
INSTRUMENTS DE VOL
PRINCIPE DU GYROSCOPE
Définition
Un gyroscope (du grec « qui observe la rotation ») est un appareil qui exploite le principe de la conservation du moment cinétique en physique (ou encore stabilité gyroscopique ou effet gyroscopique). Cette loi fondamentale de la mécanique veut qu'en l'absence de couple appliqué à un solide en rotation autour d'un de ses axes principaux, celui-ci conserve son axe de rotation invariable. Lorsqu'un couple est appliqué à l'appareil, il provoque une précession ou une nutation du solide en rotation.
Source :/fr.wikipedia.org
Principe du gyroscope
La forme la plus simple de gyroscope consiste en un disque tournant rapidement (appelé rotor). Tout rotor symétrique tournant rapidement présente des propriétés gyroscopiques. Par exemple, la terre agit comme un gyroscope, tout comme les toupies et les roues de bicyclette. L'arbre autour duquel tourne le rotor est appelé l'axe. Les gyroscopes sont définis dans leur orientation comme étant soit horizontaux soit verticaux par référence à l'axe de rotation, et non au rotor.
Les gyroscopes ont 2 propriétés de base qui les rendent importants comme base des instruments d'attitude et de direction des avions. Il s'agit de la rigidité et de la précession.
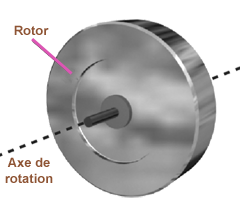
La rigidité
La rigidité ou "inertie gyroscopique" est soumise aux lois du mouvement de Newton, qui s'appliquent à l'ensemble de l'espace, et pas seulement à la Terre. Cette rigidité est la propriété du gyroscope de maintenir son axe dans une direction fixe dans l'espace, à moins d'être soumis à une force extérieure. Elle est causée par l'inertie de la masse en rotation. Pour qu'un gyroscope puisse maintenir une direction fixe dans l'espace, on utilise des dispositifs de suspension appelés cardans.
Sur le dessin ci-dessous, supposons que l'aéronef se déplace de gauche à droite c'est-à-dire que son axe longitudinal est également l'axe gyroscopique XX. Si l'aéronef s'incline à gauche ou à droite, le gyroscope reste dans la même orientation (axe de rotation horizontal et dans une direction fixe). Même chose si l'aéronef monte ou descend (axe de tangage). Cependant, si l'aéronef devait faire un virage (axe de lacet), le gyroscope et son cardan seraient forcés de sortir de leur orientation d'origine.
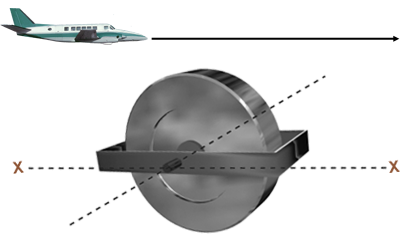
Dans ce cas, l'avion est libre en tangage ou en inclinaison sans affecter le gyroscope, mais pas en lacet. Ce systéme est appelé un systéme à un degré de liberté. La convention utilisée par l'AESA ne considère pas l'axe de rotation d'un gyroscope comme un degré de liberté.
Les cardans
En rajoutant un deuxième cardan, l'aéronef sera également libre en lacet sans perturber le gyroscope. En théorie, s'il n'y avait pas d'erreurs, le système de cardan permettait une liberté totale, et l'axe du gyroscope pointerait toujours vers un point fixe dans l'espace, indépendamment de la rotation de la terre ou du mouvement de l'avion. Sur les avions de tourisme ou bimoteurs légers les gyroscopes n'ont généralement pas plus de deux cardans..
Ci-dessous, un gyroscope avec deux cardans (interne et externe).
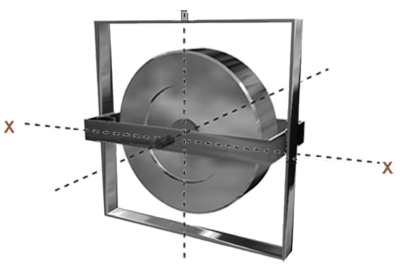
Ci-dessous, pour maintenir le gyroscope, un cadre externe a été rajouté et fixé à l'aéronef. Il se déplace donc comme l'aéronef.
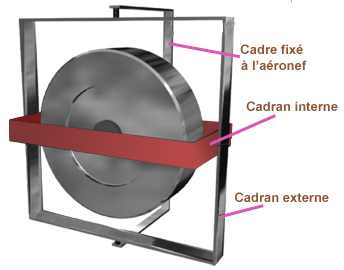
La précession
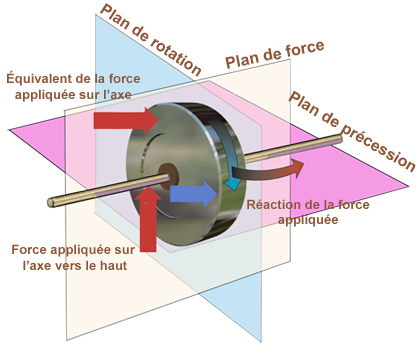
Dessin ci-dessous, le gyroscope tourne dans le sens des aiguilles d'une montre. Supposons qu'une force (couple) agisse sur l'axe de rotation vers le haut. C'est l'équivalent d'une force appuyant sur le rotor à la position 12 heures (en haut). Cependant, la réaction ne sera pas de faire tourner le gyroscope vers l'arrière autour de l'axe horizontal (XX) à partir du point où le couple est appliqué. Au lieu de cela, le couple est précontraint de 90° dans le sens de la rotation et le rotor se déplace vers la gauche (par rapport à l'axe XX) autour de l'axe vertical, comme si la force avait été appliquée à la position 3 heures.
Donc le gyroscope ne se déplace pas dans la direction de la force qu'il subit comme on s'y attend, mais dans une direction perpendiculaire.
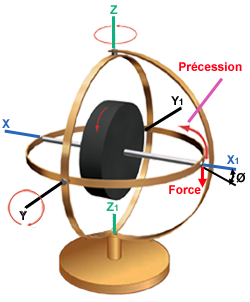
Prenons un gyroscope dont le rotor tourne autour de son axe de rotation XX. Appliquons une petite force F constante sur l'axe XX vers le bas. Au départ, l'axe du gyroscope s'incline selon un petit angle Ø et ne pointe plus vers le point fixe initial dans l'espace. Après cela, aucun autre mouvement n'a lieu autour de l'axe YY. Le couple est alors précontraint de 90° dans le sens de la rotation du gyroscope. Le mouvement de rotation commence à tourner à une vitesse constante autour de l'axe ZZ.
Si la force F est retirée, la précession cesse. Par contre, si la force F continue d'être appliquée, la rotation du gyroscope autour de l'axe ZZ continuera à tourner à une vitesse constante.
Un peu de Maths
L'équation fondamentale décrivant le comportement du gyroscope est :
`\vec {tau }=\frac {d\vec {L}}{dt}`
où les vecteurs `\vec {tau }` et `\vec {L }`sont respectivement le moment (ou couple) sur le gyroscope et son moment cinétique. Dans le cas de l'approximation gyroscopique où la vitesse de rotation `ω` est élevée, on approxime `L` par `I\vec {omega}` le scalaire `l` étant son moment d'inertie, et `\vec {omega}` son vecteur vitesse angulaire.
L'équation devient : `\vec {tau }=\frac {d(I\vec {omega})}{dt}=I\vec {\alpha }`
où le vecteur `\vec{α}` est son accélération angulaire.
Il découle de cela qu'un couple `\vec{tau }` appliqué perpendiculairement à l'axe de rotation, et donc perpendiculaire à `\vec {L}` provoque un déplacement perpendiculaire à `\vec {L}`. Ce mouvement est appelé précession.
La vitesse angulaire de la précession `Ω_P` est donnée par : `\vec {tau }= Ω_P Λ\vec{L}`
Le phénomène de précession peut être observé en plaçant un gyroscope tournant autour de son axe vertical et soutenu par le sol ou un point fixé au sol à une extrémité. Au lieu de tomber comme on peut s'y attendre, le gyroscope apparaît comme défiant la gravité en restant sur son axe vertical, même si un bout de l'axe n'est pas soutenu. L'énergie étant conservée, l'extrémité libre de l'axe décrit lentement un cercle dans un plan horizontal.
Comme le démontre la deuxième équation, sous un moment constant dû à la gravité, la vitesse de précession du gyroscope est inversement proportionnelle à son moment cinétique. Cela signifie que, comme la friction fait ralentir le mouvement tournant du gyroscope, le taux de précession augmente. Cela continue jusqu'à ce que le dispositif ne puisse plus tourner suffisamment rapidement pour soutenir son propre poids, alors il arrête la précession et tombe hors de son support.

