
POURQUOI UN AVION VOLE ?
Recherches réalisées par Frédéric Monsonnec
- Théorie basée sur l’effet ricochet.
- L’explication populaire
- Théorie basée sur l’effet Venturi
- Théorie basée sur l’effet Coanda
- Théorie de la circulation ou de Kutta & Jukowsky
- Théorie de l’écope ou de Newton.
- Théorie de Hoffman & Johnson.
Théories et théoriciens….
De nombreux chercheurs ont essayé de comprendre et de mettre sous forme d’équations la portance et la traînée. Car s’intéresser à la portance, c’est aussi découvrir comment il est possible d’obtenir un rapport portance / traînée qui soit le plus grand possible. Difficile de citer tous ceux qui ont travaillé sur la question. Voici une petite galerie de portraits de chercheurs qui par leur travail, ont permis d’avancer dans la compréhension de la portance. Même si son nom n’est pas évoqué par la suite, j’ai incorporé une photo de Sir George Cayley. Ses travaux ont fortement participé à la compréhension de la portance. Cet ingénieur anglais, que certains considèrent comme le premier vrai chercheur scientifique en aéronautique, est le concepteur du premier planeur. Il a découvert et identifié les quatre forces aérodynamiques du vol : poids, portance, traînée et poussée. La conception des avions modernes est basée sur ses découvertes, y compris les ailes cambrées !


L’explication de la portance est complexe et se prête difficilement à la simplification. Elle fait appel aux lois de Newton, aux équations de Bernoulli, celles de Navier-Stokes et d’Euler, aux travaux de Kutta-Jukowski… Rares sont ceux (dont je fais partie) qui maîtrisent ces notions.
Malgré ces difficultés, je vais essayer de présenter de manière simple, les différentes théories avancées pour expliquer le fonctionnement des ailes aériennes et sous-marines. Donc, au risque de faire des erreurs et de heurter les plus au fait de la science… Je vous l’accorde, je m’attaque à un « gros morceau » !
Parmi ces théories, certaines sont inexactes, mais elles ont leurs défenseurs. En effet, le débat sur l’origine de la portance n’est pas clos…
Le fait que certaines théories erronées restent vivaces est assez logique. Le phénomène n’est pas simple, alors lorsque vous avez découvert une explication qui semble fonctionner – et que vous la comprenez – il vous est difficile d’admettre qu’elle est incorrecte ou incomplète. Incomplète, car bien souvent ces théories se basent sur un ou plusieurs phénomènes bien réels.
Un petit rappel sur la terminologie
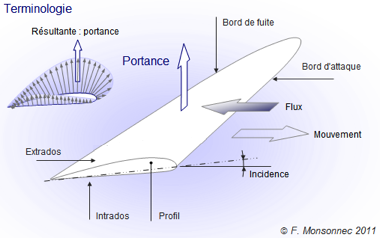
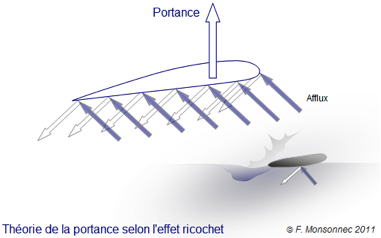
Théorie basée sur l’effet ricochet.
La portance a pendant longtemps été expliquée comme étant semblable au phénomène qui permet à un joli caillou plat, manipulé par une main experte, de faire un pied de nez à Archimède !
Cette théorie du ricochet est basée sur l’idée que la portance serait due à l’énergie développée par les molécules qui « frappent » le dessous du plan porteur. Elle fait référence à la troisième loi de Newton : lorsqu’un solide A exerce une force sur un solide B, le solide B exerce sur le solide A la force directement opposée. Même si, dans le cas de la « pierre surfeuse », l’explication fait appel à bien d’autres lois de la physique…
Oui mais
Cette explication ne prend en compte que l’interaction du fluide avec la surface inférieure de l’aile. Elle suppose que toute la portance est générée par l’intrados, ce qui est totalement erroné. Il a été démontré qu’environ 75 % de la portance est liée à l’extrados (pourcentage bien entendu fonction de nombreux éléments comme la forme du profil).
Remarque
Dans des cas très particuliers, comme certains régimes de vol où la vitesse est très élevée et la densité de l’air très basse, une faible quantité de fluide est en contact avec l’extrados. Dans ce cas, une partie de la portance est bien fonction de la capacité du plan porteur à « ricocher » !
Ces conditions sont celles de la navette spatiale pendant une partie de la phase d’entrée dans l’atmosphère (conditions hypersoniques).
Sans oublier d’autres engins qui utilisent la même capacité à « ricocher », le XB-70 Valkyrie et le X-43 A, dont Gurval a déjà parlé dans son excellent article, La ventilation : Un peu d’air dans ce monde de fluide.
L’explication populaire.
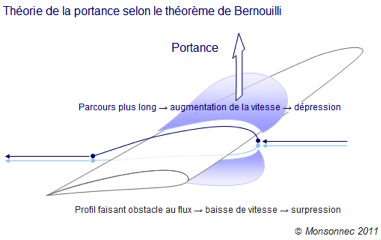
Cette théorie basée sur le théorème de Bernoulli peut aussi être appelée « théorie du temps de transit équivalent ». Cette explication est celle qui est la plus souvent avancée par ce qu’elle est simple à comprendre. Cette thèse s’appuie sur le fait que, dans la majorité des cas, la partie supérieure des ailes (extrados) a une longueur supérieure à celle de la partie inférieure (intrados). Imaginons deux molécules qui seraient séparées par le bord d’attaque de l’aile. La molécule qui passe au-dessus de l’aile, va parcourir plus de distance que son « ex-voisine » qui passe en dessous du profil. En se basant sur le fait que la nature a horreur du vide (même ce point est décrié, et à juste titre !), il nous est expliqué que ces deux molécules devraient se retrouver en même temps derrière le profil. Pour ce faire, celle qui a été dirigée vers la voie supérieure, devrait voir sa vitesse augmenter pour être à l’heure au rendez-vous.
Le théorème de Bernoulli dit qu’à altitude égale, la pression d’un fluide diminue quand sa vitesse augmente et inversement. La survitesse sur l’extrados entraînerait donc une dépression (aspiration). De plus, la molécule qui elle se déplace sur l’intrados voit sa vitesse ralentir (puisque le plan porteur représente un obstacle), ce qui engendre une surpression.
Oui mais
La loi décrite par Daniel Bernoulli, qui traduit le principe de la conservation de l’énergie dans les fluides, intervient bien dans le phénomène qui nous intéresse. Mais cette explication, bien trop souvent citée, est trop simple pour être complète ! Un avion disposant d’ailes planes peut voler, de même que les avions munis d’ailes au profil symétrique (donc avec une même corde sur l’intrados et l’extrados).
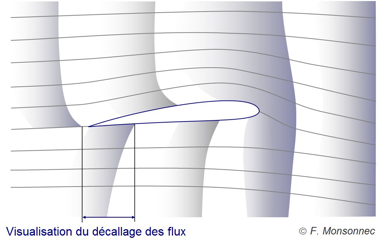
Enfin, des essais en tunnel ont montré qu’en réalité le courant de l’extrados arrive avant celui de l’intrados !
Théorie basée sur l’effet Venturi
Les défenseurs de cette théorie mettent en avant l’idée que la surface supérieure d’une aile agirait comme un venturi qui accélèrerait le flux. Cet effet bien réel porte le nom de son découvreur, Giovanni Battista Venturi. Le théorème de Bernoulli permet d’expliquer ce phénomène : puisque le débit de fluide doit être constant (la nature a horreur…) et que la surface de passage diminue, la vitesse augmente nécessairement (du fait de la conservation de l’énergie). L’augmentation d’énergie cinétique se traduit par une diminution d’énergie élastique, c’est-à-dire une dépression. Notre plan porteur faisant obstacle au flux, il y aurait resserrement du flux et augmentation de la vitesse sur la partie supérieure du plan. Il découlerait de l’accroissement de la vitesse une pression inférieure sur l’extrados, d’où création de portance…
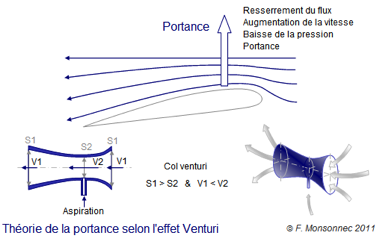
Oui mais
Cette théorie, qui rejoint celle de Bernoulli, est basée sur l’idée qu’un plan porteur agirait comme un col venturi. Avec une surface de départ (ou zone de passage du flux) importante, une surface diminuée et enfin, de nouveau, une augmentation de la surface. Mais un plan porteur n’est pas un col venturi. Il n’y a aucune autre surface pour représenter l’autre moitié du col ! Certains documents avancent le fait que les « couches d’air » supérieures remplaceraient l’absence de surface au-dessus du plan pour matérialiser le col venturi ! Cette théorie impose un resserrement du flux, ce pourrait être le cas sur l’extrados, avec un resserrement entre le bord d’attaque et la zone d’épaisseur maximum, mais ce ne l’est pas le cas sur l’intrados d'un profil asymétrique. Intrados qui entre tout de même pour ¼ dans le développement de la portance.
Si vous doutez encore de l’inexactitude de cette théorie, sachez qu’il a été démontré qu’une plaque plane peut générer de la portance (au prix d’une forte traînée, c’est vrai). Dans ce cas, l’effet venturi serait complètement absent puisqu’il n’existe aucun resserrement ! Et pourtant, il est possible de faire voler un « avion » muni de surfaces portantes plates : comme un fer à repasser volant ou une tondeuse à gazon !

Théorie basée sur l’effet Coanda
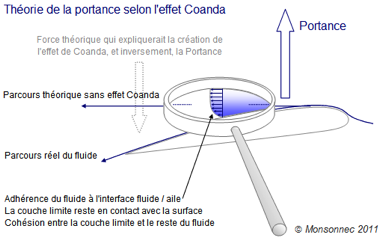
Cette théorie suggère que la portance, est liée à l’effet Coanda. Effet mis en évidence et décrit par l’Ingénieur Roumain Henri Coanda, que certains surnomment le père de l’aviation à réaction. Dans certaines conditions, un flux d’air ou d’eau qui se déplace à proximité d’une surface courbe adhérera à cette surface et la suivra. L’argument principal de cette théorie, est que si le fluide change de direction, alors il doit exister une force extérieure qui explique ce déplacement. Il nous a ensuite expliqué que cette force est liée à la combinaison de la différence de pression et à la viscosité du fluide.
Pour en revenir à l’effet Coanda, lorsque l’on cherche à déterminer l’origine de ce phénomène, on découvre beaucoup d’expériences qui permettent de le visualiser, mais pas ou peu d’explications ! L’effet Coanda semble être une combinaison de deux facteurs : les efforts de frottement à la surface et la viscosité du fluide. La tension superficielle, ou les forces de Van Der Walls, ralentissent le fluide à son interface avec l’aile et conservent la couche limite en contact avec la surface. La viscosité du fluide permet la cohésion entre la couche limite et le reste du fluide. Bien entendu, ceci n’est valable que dans une certaine plage de conditions : viscosité, vitesse, courbure…
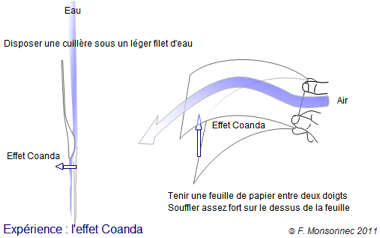
Expériences
Il suffit de disposer un verre ou une petite cuillère sous un robinet, de façon à ce qu’un filet d’eau touche la partie bombée de l’objet, pour voir le liquide suivre la surface de l’ustensile. Il existe aussi une autre expérience, très facile à réaliser, celle de la feuille de papier légèrement courbée, tenue entre 2 doigts, et au-dessus de laquelle on souffle. Si on souffle fort, le papier s’élève.

Oui mais
Nous savons que pour qu’il y ait effet Coanda, il faut que la forme soit convexe, pourtant une plaque plane est capable de produire de la portance !
Bien que d’autres théories plus abouties intègrent l’effet Coanda dans l’explication de la portance, ce seul effet ne peut pas expliquer ce phénomène.
D’après cette théorie, si la viscosité est modifiée, la portance est proportionnellement modifiée. Toutefois, en réalité, le niveau de portance produit par une aile est indépendant de la viscosité (sur une importante plage).
Cette théorie, seulement basée sur l’effet Coanda, néglige le fait que l’aile augmente la vitesse du fluide à son voisinage et ne tient compte que de la vitesse relative du fluide, donc à une certaine distance du profil. De ce fait, les partisans de cette solution obtiennent des résultats environ 10 fois plus faibles que la réalité.
Remarque :
L’expérimentation par Henri Coanda du premier moteur à réaction ne manque pas de piquant (ou de chaleur !). 20 ans après cet essai, Henri Coanda comprit ce qui s’était passé lors de son premier essai de moteur à réaction, et durant 35 ans, il étudia ce phénomène et déposa de nombreux brevets.
Théorie de la circulation ou de Kutta & Jukowski
Les premières recherches effectuées dans le but de quantifier la portance ont été réalisées sur la base d’un fluide parfait. Nous allons le voir, cela a amené les chercheurs devant une incompréhension, puisque leurs travaux ne rejoignaient pas les observations.
Pour bien comprendre cette théorie, et ce que le fluide nous cache (!), il est judicieux de partir de cette même hypothèse. La simulation du flux d’un fluide parfait – incompressible et sans viscosité – autour d’une plaque de faible épaisseur montre que, pour ces conditions, il existe deux lignes de séparation du flux (appelées aussi ligne de stagnation et point d’arrêt, lorsqu’il s’agit du point sur le plan). Une ligne sur l’intrados un peu en dessous du bord d’attaque, la seconde (qui pourrait être appelée ligne de jonction), sur l’extrados un peu au-dessus du bord de fuite.
Cette simulation montre surtout que les lignes d’écoulement sont symétriques par rapport au plan. Les forces de pression des deux côtés de la plaque sont identiques, sans portance et sans traînée ! Ce résultat, est bien entendu, totalement à l’opposé de la réalité. Là où « le bât blesse », c’est que nous sommes partis de l’hypothèse que la viscosité du fluide était nulle. Cet écart entre la théorie de l’époque (18ème siècle) et la réalité porte le nom de son découvreur, le paradoxe d’Alembert.
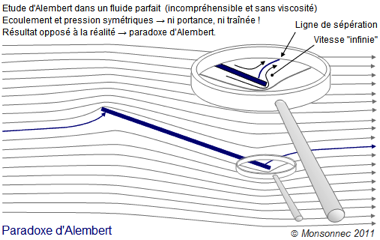
Dans les écoulements réels, des perturbations apparaissent à l’arrière du solide (sillage). L’origine de ces perturbations est la viscosité des fluides réels. Sans viscosité, pas de traînée. C’est grâce aux travaux de W. Kutta et N. Jukowski au début du 20ème siècle, que le mystère s’est éclairci : il existerait un phénomène autour du profil nommé circulation. À noter que Kutta et Jukowski sont arrivés aux mêmes conclusions alors que leurs études ont été réalisées par des voies indépendantes.
Quelques années plus tard, en 1918, le physicien allemand Prandtl (que certains appellent le père de la théorie moderne de la mécanique des fluides et à qui on doit la notion de couche limite), a donné une description plus complète de cette possible circulation (d’après les Anglais, c’est Frederick William Lanchester, qui a travaillé sur ce point avant Prandtl). La circulation apporterait l’élément manquant pour comprendre comment se développe la portance.
À noter que cette théorie de la circulation avait déjà été évoquée par Robin puis par Magnus.
Que propose la théorie de Kutta-Jukowski ? Lorsqu’un corps symétrique à forme lisse, comme un plan de section ovale, se déplace dans un fluide avec une incidence positive, il y a deux points d’arrêt. Le premier près du bord d’attaque sur l’intrados, le second sur le bord de fuite de l’extrados (comme notre plaque dans un fluide parfait, voir ci-dessus). La circulation est nulle, la portance aussi.
Maintenant, d’après WK et NJ, si un profil avec un bord de fuite aigu se déplace dans un fluide avec une incidence positive, les deux points d’arrêt se trouvent au départ dans les mêmes positions que précédemment. Quand le fluide qui passe sous l’intrados atteint le bord de fuite, il doit contourner celui-ci pour aller vers le point d’arrêt situé sur l’extrados. En raison du rayon de courbure nul du bord de fuite, la vitesse du flux devrait être localement infinie. Ce qui est bien entendu impossible.

Le bord de fuite aigu génère toutefois une vitesse élevée qui se transforme en un tourbillon initiateur. Telle la roue dentée d’un engrenage, le tourbillon entraînerait par viscosité le fluide avoisinant, générant une « circulation » autour du plan. La circulation du tourbillon initiateur serait équilibrée par celle du tourbillon attaché au plan (qui tourne en sens inverse). D’après la théorie de Kelvin, la circulation autour d’une courbe fermée doit rester nulle.
Lorsque le premier tourbillon croît, le second croît dans les mêmes proportions, ce qui déplace le tourbillon initiateur vers le bord de fuite où il quitte le profil avant d’être dissipé : l’équilibre est atteint (l’influence du tourbillon initiateur devient négligeable). La circulation autour du profil s’adapterait constamment de telle sorte que la condition de Kutta-Jukowski reste vérifiée.
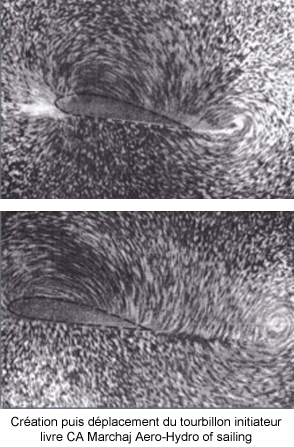
À chaque évolution de l’incidence ou de la vitesse qui modifie la circulation, un nouveau tourbillon initiateur se forme et se détache du profil. Ces tourbillons bien réels, permettraient d’obtenir un nouvel équilibre de la circulation. Cela reviendrait à ajuster la circulation de manière à permettre à la ligne de courant de s’échapper du profil en partant de sa pointe sans que celle-ci soit contournée.

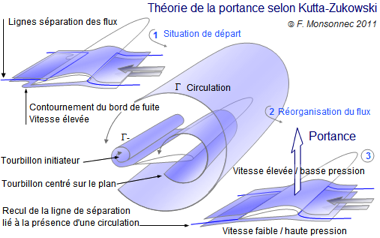
Le déplacement du point d’arrêt jusqu’au bord de fuite stabilise l’écoulement. Sur l’extrados, la vitesse du plan et la circulation s’ajouteraient. Sur l’intrados, la circulation serait opposée à la vitesse du profil. La circulation autour du profil se traduirait par des vitesses plus élevées sur l’extrados, que sur l’intrados, d’où des pressions plus faibles, donc par la portance (voir théorème de Bernoulli).
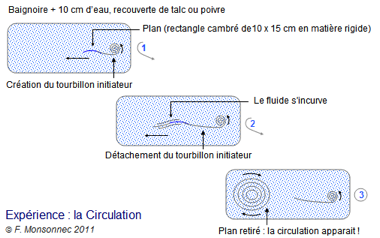
Expérience
Remplir une baignoire de 10 cm d’eau et saupoudrer la surface de talc ou de poivre (cela doit fonctionner avec d’autres poudres, mais éviter celle de Colombie sous peine d’effets secondaires !). Découper ensuite un rectangle de 10 x15 cm dans une matière rigide (carton…), que vous cambrez légèrement. Déplacer la plaque cambrée, le « plan », de la droite vers la gauche de la baignoire. Vous pourrez alors observer : la création du tourbillon initiateur, le détachement du tourbillon initiateur, le fait que l’eau en avant du profil s’incurve vers le haut pour passer au-dessus du profil. À environ 30 cm de l’extrémité de la baignoire, vous pouvez retirer le plan de l’eau et la circulation apparait !!!
Comment résumer cela ?
De part, sa forme (bord de fuite tranchant), un profil disposé avec une certaine incidence « oblige » le flux à se positionner de manière à ce que la ligne de séparation des flux venant de l’intrados et de l’extrados se place au niveau du bord de fuite. Ce déplacement est lié au développement d’un tourbillon généré, au démarrage, par le flux qui contourne le bord de fuite. Ce tourbillon fait naître un second tourbillon centré sur le plan. Ces deux tourbillons donnent naissance à un phénomène de circulation autour de l’aile qui permet d’obtenir un équilibre du système. Le flux, une fois stabilisé, il existe une différence de vitesse et de pression entre l’intrados (haute pression*) et l’extrados (basse pression*) et donc création d’une portance.
Remarques
D’après cette théorie, la portance est donc intimement liée au caractère anguleux du bord de fuite. Mais cela fonctionne aussi avec des profils aux deux extrémités aiguës comme ceux utilisés sur Mayfly, Icarus… (profils lenticulaires)
Pourquoi, alors que les pionniers de l’aviation n’étaient pas au courant de l’existence de ces phénomènes et de l’importance de la forme du bord de fuite, les premiers profils ont été réalisés avec un bord de fuite en « pointe » ? Sûrement parce que leurs travaux découlaient de l’observation de la forme des ailes d’oiseaux…comme ceux d’Otto Lilienthal.
Oui mais
Et bien, il y a plusieurs « Oui mais », qui sont pour certains développés dans une des théories suivantes. Lorsque j’ai essayé de comprendre cette théorie, la partie la plus difficile à intégrer était la notion de circulation. Notion difficilement visualisable…
Certaines sources, présentent la circulation comme une sorte de courant circulaire autour du plan porteur. D’autres expliquent que la vitesse de chaque particule est proportionnelle à sa distance avec le centre de la circulation (située au niveau du plan porteur). La circulation pourrait donc être présentée comme le produit de V (la vitesse) par D (la distance) des molécules. Ce calcul tiendrait compte du sens de l’écoulement et la circulation pourrait être « visualisée » autrement que comme un courant circulaire dans lequel s’inscrit le plan porteur. Mais cette fameuse circulation reste tout de même assez abstraite…
Pour certains, la notion de circulation ne serait qu’un artifice mathématique développé pour que la solution des équations soit correcte ! Ils avancent qu’il n’existerait pas de mécanisme physique qui expliquerait ce phénomène et d’observations pour prouver qu’il existe réellement un flux se déplaçant à contre-courant sur l’intrados !
Théorie de l’écope ou de Newton
Cette théorie plus récente, et mise en avant (entre autres) par David Anderson et Scott Eberhardt, fait appel à la notion « d’écopage » du fluide. Elle est aussi appelée théorie du flux descendant (traduction personnelle de Downwash) ou théorie basée sur la 3ème loi de Newton.
Le fluide qui passe autour d’une aile, disposée dans le flux avec une incidence positive, est dévié vers le bas. Cette déviation du fluide est générée par l’intrados, mais aussi par l’extrados ! En contournant la partie supérieure du profil, et en raison de sa viscosité, l’air ou l’eau en contact avec le profil, entraîne avec lui les couches supérieures du fluide.
Nous l’avons vu, ce phénomène s’appelle l’effet Coanda. Dans le domaine du plus lourd que l’air, certains utilisent le terme « d’écope » ou de « pompe » pour décrire le phénomène généré par un plan porteur. Pour éviter la formation de vide derrière l’obstacle dans certains cas, la nature a vraiment horreur du vide ! Une certaine quantité de fluide est « tirée » et accélérée du haut (partie située au-dessus du profil) vers le bas (derrière le profil). Le travail nécessaire pour faire descendre et accélérer les molécules (qui ont une masse) expliquerait donc la portance : le déplacement des molécules situées au-dessus du plan occasionnant une dépression, donc « l’aspiration » du plan porteur.
D’ailleurs, ce déplacement d’une certaine quantité de fluide vers le bas est logique puisque la portance occasionne un déplacement du plan porteur vers le haut, il faut bien qu’une partie du fluide soit dirigée vers le bas (d’où l’appellation par certains de théorie de Newton : action / réaction).
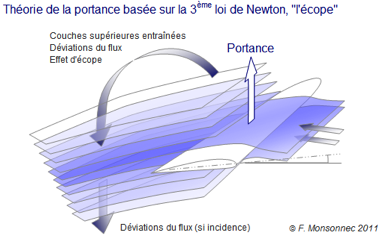
Un bon moyen pour expliquer cette théorie, est peut-être une explication par l’absurde (merci Xavier). Si l’air ne suivait pas le contour du profil, une poche de vide se créerait derrière celui-ci. D’où la création d’une dépression qui attirerait les molécules présentes au dessus du plan pour combler la poche de vide ! La dépression sur la partie arrière du profil dévierait donc le flux. Mais nous l’avons vu, le fluide suit bien les contours du plan porteur, ce qui génère un déplacement des molécules et la portance.
Certains pourraient me rétorquer : « d’accord pour la partie en arrière du point d’épaisseur maxi, mais que se passe t’il avant ? ». Le plan se déplace à une certaine vitesse dans l’air ou l’eau. Avant d’arriver sur l’aile, une portion du fluide est déviée vers le haut, en raison de la présence d’une zone de surpression sur l’intrados. Cette zone de dépression au-dessus de l’aile renforce ce phénomène, ainsi que le mouvement aval des molécules crée une dépression qui attire et accélère les molécules en amont.

Remarques
Plus l’incidence est importante, plus « l’obstacle » est grand, donc la déviation du fluide aussi (avec une certaine limite : le décrochage). L’incidence est un élément important dans la création d’une portance, mais elle n’est pas obligatoire ! Un profil asymétrique génère de la portance même à incidence nulle. Il faut d’ailleurs le caler en incidence négative pour que la portance soit nulle, c’est son angle d’incidence neutre.
La portance d’une aile serait donc proportionnelle à la quantité de fluide déviée vers le bas. Les avions de voltige volent sur le dos avec une forte incidence et leurs ailes sont symétriques ou presque. En vol normal, ils n’ont même pas besoin de cabrer leurs volets de bord de fuite pour générer de l’incidence ou de la portance (sauf à faible vitesse, comme tous les profils).
Oui mais
Et bien, il semble une nouvelle fois que l’explication soit incomplète, car d’autres théories existent. Bien entendu, cette explication est satisfaisante même pour un avion qui vole sur le dos. Pourtant, même s’il est indéniable que le fluide est dévié vers le bas, cette théorie ne serait, d’après ceux qui la critiquent, pas suffisante pour expliquer certains phénomènes (effet de sol…). Elle ne permettrait pas de quantifier la portance, juste d’expliquer ce qui se passe autour de l’aile. Elle n’expliquerait pas ce qui se passe, par exemple, sur le bord de fuite… Autre question, pourquoi le fluide va plus vite sur l’extrados… ?
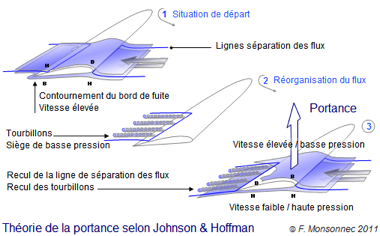
Théorie de Hoffman & Johnson
Cette théorie, développée par Johan Hoffman et Claes Johnson (deux Suédois), présente une nouvelle explication mathématique et physique de la création de la portance et de la traînée ainsi qu’une nouvelle résolution du paradoxe d’Alembert. Elle est basée sur de nouvelles découvertes de la dynamique des fluides turbulents (études réalisées à partir de solides évoluant dans l’air). Découvertes obtenues grâce au traitement informatique d’un modèle mathématique : les équations de Navier-Stokes & d’Euler. Ce travail tend à prouver que les précédentes théories sont incorrectes.
D’après J.H. & C.J., la théorie la plus avancée, et qui pour certains est l’état de l’art – théorie de Kutta-Zhulovsky – est une théorie « simpliste » qui permet d’expliquer la portance seulement dans une fourchette de conditions restreinte. Cette théorie ne donnerait pas d’explication pour la portance et la traînée pour des profils en 3 dimensions, dans un flux turbulent et dans un fluide légèrement visqueux. Par exemple, ce qui se passe autour de l’aile d’un jumbo-jet en phase de décollage avec un angle d’incidence important. Enfin et surtout, le flux circulant autour de l’aile ne serait que purement fictif. J.H. & C.J. avancent que cette étude du flux dans la théorie de Kutta-Zhulovsky est faite de manière bidimensionnelle alors qu’en réalité, le flux est tridimensionnel et turbulent.
Cette théorie se base sur l’importance des tourbillons disposés le long du bord de fuite du profil (mais qui n’ont rien à voir avec le vortex présent à l’extrémité d’une aile). Ces tourbillons ont une forme similaire à celle que l’on peut découvrir lors de la vidange d’une baignoire. On peut observer la dépression de la surface libre qui se forme au-dessus de l’orifice de vidange. Cette dépression reflète une chute de pression au sein du liquide. Les tourbillons se développent quand les flux de l’extrados et de l’intrados se rejoignent sur le dessus de l’aile un peu avant le bord de fuite. Là où la théorie de Kutta-Zhulovsky donnait naissance à un tourbillon dont les génératrices étaient parallèles au bord de fuite, cette théorie se base sur le développement de tourbillons, partant de la même zone, mais perpendiculairement au bord de fuite.
Ces tourbillons sont d’abord retardés, ensuite accélérés et étirés dans la direction du flux. À l’intérieur des tourbillons, la pression est basse. Cette basse pression neutraliserait la haute pression présente sur le dessus du plan et modifierait la distribution de la pression du flux sur le bord de fuite. Ces tourbillons permettraient donc de plaquer le fluide sur l’extrados. Cet effet, qui d’après JH et CJ n’est pas lié à l’effet Coanda, permettrait au flux de quitter l’aile en suivant la direction donnée par la partie terminale de l’extrados (et non plus depuis la ligne d’arrêt théorique). Ce mécanisme génèrerait donc la portance, mais aussi la traînée (tourbillons) et le déplacement d’une certaine quantité de fluide vers le bas (effet d’écope).
Johan Hoffman & Claes Johnson ont réalisé des simulations numériques à partir d’un profil 3D type Naca 0012 (symétrique). Ces tests démontrent d’après eux 2 régimes : un pour les angles d’incidence entre 0 à 16°, le second de 16° à 20°. Le premier régime, de 0 à 16°, peut être scindé en 2 zones : 0 à 4/6 et 4/6 à 16. Pour la zone 0 à 4/6 la portance augmente de façon presque linéaire en fonction de l’incidence avec un rapport portance / traînée qui monte progressivement jusqu’à 13 (plus ce rapport est grand, plus l’efficacité est grande). Pour la seconde, 4/6 à 16°, la progression est elle aussi presque linéaire mais plus rapide. Par contre, le rapport portance trainée chute rapidement jusqu’à 7. Ce rapport s’effondre à 3 à 20°.
Que se passe t’il physiquement d’après eux ?
- Phase 1 – 0 à 4/6°
Faible traînée en raison de la présence des vortex longitudinaux (basse pression) liés au bord de fuite. Les tourbillons longitudinaux attachés au bord de fuite restent constants en force, mais remontent graduellement sur la surface supérieure. La traînée n’augmente que lentement.
- Phase 2 – 4/6 à 16°
La basse pression située au-dessus du bord d’attaque augmente, ce qui évite la séparation et augmente la portance dans cette zone.
La haute pression sur le bord d’attaque de l’intrados se déplace vers l’arrière et la pression augmente lentement, ce qui contribue à la portance.
La traînée sur l’extrados est proche de zéro en raison de la succion sur le bord de fuite.
Par contre la traînée augmente sur l’intrados,
- Phase 3 – 16 à 20°
Cette phase est celle qui génère le plus de portance juste avant le décrochage de l’aile avec de fortes perturbations sur l’extrados et dans son sillage, ce qui génère aussi une forte trainée.
Comment résumer cela ?
De par sa forme (bord de fuite tranchant), un profil disposé avec une certaine incidence « oblige » le fluide à se positionner de manière à ce que la ligne de séparation des flux venant de l’intrados et de l’extrados se place au niveau du bord de fuite. Ce déplacement est lié au développement de multiples tourbillons (perpendiculaires au profil) engendrés par l’instabilité du flux lorsqu’il contourne le bord de fuite. Ces tourbillons de basse pression engendrent aussi la traînée. Le flux, une fois stabilisé, il existe une différence de vitesse et de pression entre l’intrados (haute pression) et l’extrados (basse pression), d’où la création de la portance. Le mécanisme d’instabilité est fondamental, il modifie le flux sur l’arrière de l’extrados, mais ne modifie pas celui du bord d’attaque qui développe déjà une portance positive. Ainsi, la portance est liée à la traînée, pas de portance sans traînée.
Oui mais
Les défenseurs de la théorie de Kutta & Jukowski pensent que le travail d’Hoffman & Johnson n’apporte rien de nouveau, et que la circulation est une réalité physique. Ils s’appuient, entre autres, sur le fait que pour mettre en œuvre les solutions numériques, il faut indirectement accepter la notion de circulation, puisqu’il serait nécessaire de préciser que le système accepte la condition de Kutta, en précisant dès le départ que le flux quitte au bord de fuite.
Pour eux, les calculs numériques sont trop souvent utilisés sans vérification expérimentale. L’utilisation de ce type d’outil nécessite une bonne compréhension de ce qu’ils peuvent ou ne peuvent pas faire, ce qui demande une grande expérience. De plus, un comparatif de différents programmes de simulation a montré que ces outils peuvent donner des résultats opposés en raison des différentes hypothèses choisies. Pour certains défenseurs de la théorie de la circulation, les écrits d’Hoffman & Johnson auraient surtout pour but de réfuter la théorie de circulation au moyen d'observations erronées. Hoffman & Johnson répondent que cette nouvelle théorie remplace la circulation par d’autres phénomènes physiques réels.
Conclusion
L’explication de la portance fait appel à des notions complexes et difficiles à simplifier. Certaines théories sont inexactes, mais ont leurs défenseurs : le débat sur l’origine de la portance n’est pas clos.
Deux théories s’opposent :
- Celle basée sur le théorème de Bernoulli qui se base sur le fait que, dans la majorité des cas, la face supérieure d’une aile a une longueur supérieure à la face inférieure. La molécule qui passe au-dessus de l'aile, va parcourir plus de distance qu’une seconde qui passe sous le profil. En se basant sur le fait que la nature a horreur du vide, ces deux molécules devraient se retrouver en même temps derrière le profil. Celle dirigée vers la voie supérieure (extrados), devrait voir sa vitesse augmenter. Suivant le théorème de Bernoulli, la vitesse augmentant, la pression diminue, d’où création d’une portance (et inversement sur l’intrados). Toutefois, des mesures en laboratoire ont démontré l’invalidité de cette théorie.
- Celle basée sur une des lois de Newton met en avant le fait que l’aile occasionne un déplacement du fluide (le plus souvent vers le bas), du fait de sa forme et de son incidence (angle formé par l’aile et direction). Comme à toute action existe une réaction, le plan porteur serait par conséquent aspiré en sens inverse.
Deux autres théories complexes se rajoutent à ces deux premières, elles tentent surtout d'expliquer les phénomènes qui se passent sur la partie arrière du plan porteur (théorie de Kutta- Jukowski et la théorie d’Hoffman & Johnson). L’essentiel est de comprendre que l’aile des oiseaux ou d’un avion, la voile, la quille, le safran d’un bateau, fonctionne comme une « écope » qui déplace un certain volume de fluide et est, par réaction, aspiré en sens inverse.
J’ai essayé de présenter les différentes théories que l’on peut trouver sur internet et dans la littérature (peut être pas toutes, mais déjà un certain nombre). J’ai trouvé des critiques pour l’ensemble des théories avancées. J’ai essayé de démêler le « faux du vrai ». Pourtant, je n’ai pas vraiment de certitude.
Je vous laisse faire votre propre choix dans cette collection de théories… Vous avez peut-être deviné celle qui me satisfait le plus ?
![]()

