
LES HELICES
- Pas d"une hélice
- Fonctionnement aérodynamique
- Les différentes hélices
- Les différents calages
- Hélice nouvelle génération
But
Le but de l'hélice est de fournir une force de traction en prenant appui sur l'air.
Profil d'une pale
Le profil d'une pale d'hélice ressemble au profil d'une aile, c'est-à-dire doté d'un bord d'attaque, d'un bord de fuite, d'une corde de référence, d'une épaisseur moyenne, d'une cambrure, etc. Il détermine les performances d'une hélice, mais aussi sa résistance. L'optimisation de la géométrie d'une pale est donc un compromis entre performance et résistance mécanique.
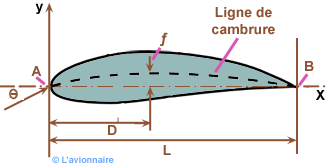
`A` = Bord d'attaque
`B` = Bord de fuite
`L` = Corde de référence
`D` = Position de la cambrure maximale du profil
`ƒ` = Cambrure maximale
`θ` = Angle de calage
Vrillage et angle de calage
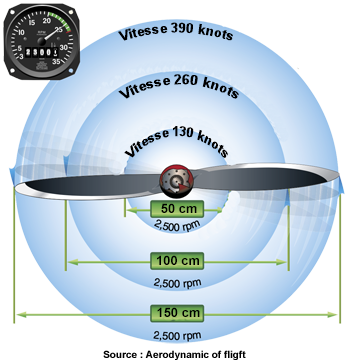
La raison pour laquelle une hélice est " vrillée " est que les parties extérieures des pales de l'hélice, comme toutes les choses qui tournent autour d'un point central, se déplacent plus rapidement que les parties situées près du moyeu. Si les pales avaient le même pas géométrique sur toute leur longueur, les parties situées près du moyeu pourraient avoir un angle d'attaque négatif alors que les extrémités des hélices seraient calées à la vitesse de croisière.
Vitesse de la pale en fonction de la distance par rapport au moyeu pour un régime moteur de 2500 tours/minute.
Le vrillage de la pale de l'hélice est l'angle entre la corde du profil de bout de pale et la corde du profil de pied de pale (dessin ci-dessous). Ce vrillage permet à l'hélice de fonctionner avec un angle d'incidence relativement constant sur toute sa longueur en vol de croisière.
L'angle de calage `θ` est défini entre la corde de référence du profil et le plan de rotation.
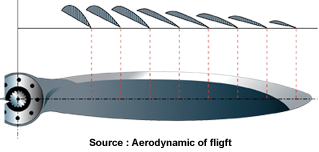
L'épaisseur et la forme de la pale varient pour permettre de régler l'angle d'incidence des profils en fonction de la variation des angles apparents perçus par les profils du pied au bout de la pale.
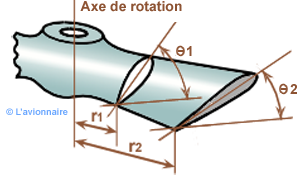
Pas d'une hélice
Pas géométrique, pas relatif, pas effectif
Le pas géométrique est la distance parcourue par l'hélice en un tour suivant l'axe de rotation de l'hélice. C'est-à-dire la distance séparant deux points sur une génératrice du cylindre.
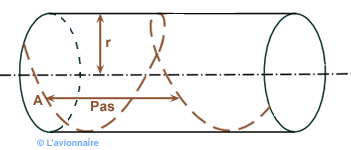
En développant une section d'hélice, on constate que le point A a subi une translation H pour une rotation d'un tour.
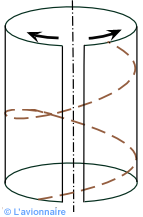
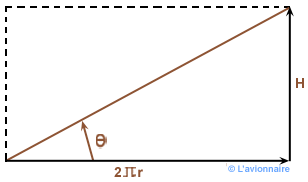
Cette translation `H` appelée pas théorique est la valeur de la translation de l'hélice pour une rotation complète dans un milieu incompressible et inerte et s'écrit `H = 2 π. r . tan θ`.
Le pas géométrique de l'hélice est défini généralement comme étant le pas de la section située à une distance de `r = 0,7 R ` de l'hélice, elle est appelée section de base.
Le pas relatif est le rapport :
`h = \frac{H}{D} = \frac{pas géométrique}{diamètre de l'hélice}`
`h = \frac{2 π. 0,7 Rtan θ}{2R} = 2,2 tan θ` pour `θ` à `0,7 R`
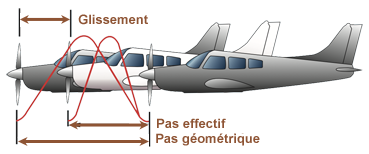
Le pas effectif est la distance effectivement parcourue par l'avion pendant un tour d'hélice. En effet, l'hélice peut tourner sans que l'avion avance (Cas d'un point fixe).
Le glissement
Le glissement de l'hélice est la différence entre le pas géométrique de l'hélice et son pas effectif. Ainsi, le pas géométrique ou théorique est basé sur l'absence de glissement, mais le pas réel ou effectif inclut le glissement de l'hélice dans l'air.
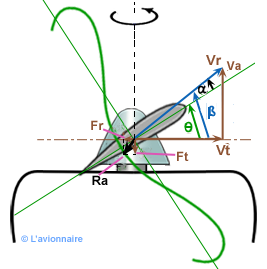
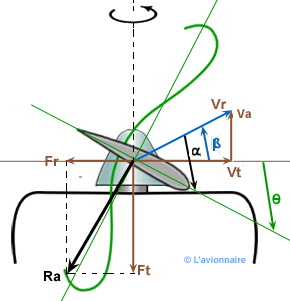
Fonctionnement aérodynamique
Prenons un élément de pale situé à r de l'axe de l'hélice.
Nous avons :
`θ` = angle de calage
`β` = angle d'avancement
`α` = angle d'incidence
Le point `A` du profil de référence d'une pale d'hélice en mouvement est soumis à deux vitesses :
- `Vt` vitesse tangentielle, égale à `2 π .r.n ` (n étant la vitesse de rotation en tours/s).
- `Va` vitesse en translation en m/s, c'est la vitesse d'avancement ou vitesse de l'avion.
- Il en résulte un mouvement suivant le vecteur `Vr`.
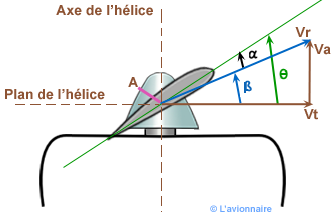
Comme pour l'aile, une section de pale d'une hélice attaque l'air suivant un angle d'incidence `α` et va développer une résultante aérodynamique `Ra` qui se décompose :
- Une force de traction `Ft` suivant l'axe de l'hélice et dans le sens du mouvement.
- Une force de résistante `Fr` opposée à la rotation et à l'origine d'un couple résistant.
En régime stabilisé ce couple résistant `Cr` sera égal et opposé au couple moteur `Cm`.
D'autre part, l'incidence `α` va varier à la fois en fonction de la vitesse de rotation et de la vitesse sur trajectoire de l'avion.
Le recul est la différence entre le pas géométrique et le pas réel.
- Pas géométrique `H = 2 π.r.tanθ`
- Pas réel ou avance par tour `H' = 2 π. r. tan β` avec
Donc le recul est la différence entre `tan θ` et ` tanβ` soit l'incidence ` α` qui est à l'origine de `Ra` (résultante aérodynamique) donc de la traction.
Visualisation du sillage laissé par une hélice.

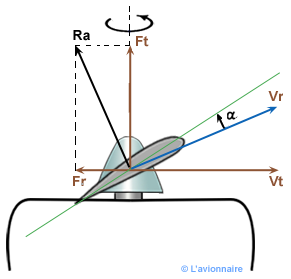
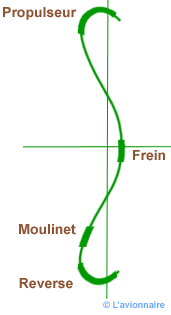
Fonctionnement propulseur
L'hélice fournit une traction et consomme de la puissance moteur.
`α` est > 0.
`Ft` est > 0.
`Fr` est > 0.
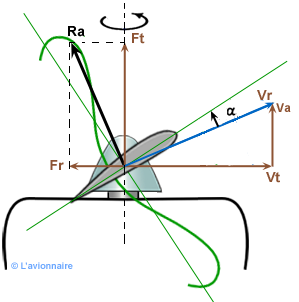
Fonctionnement moulinet
L'hélice fournit une traction négative et un couple moteur. Cette position permet de dévirer une hélice pour remise en marche du moteur.
`α` est négatif.
`Ft` est < 0.
`Fr` est < 0.
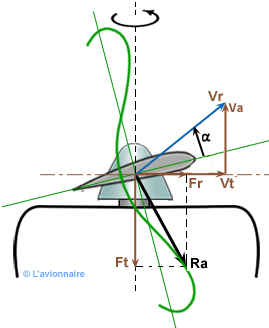
Fonctionnement drapeau
`θ` est à 90°. La pale est dans le lit du vent relatif
`Ft` est réduit à sa plus petite valeur.
`Fr` est nulle. La pale est immobile.
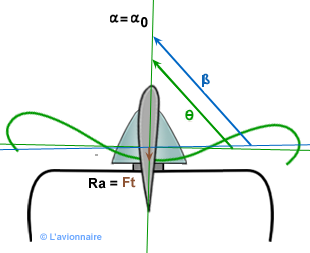
Fonctionnement frein
L'hélice fournit une faible traction négative qui à tendance à freiner l'avion.
`α` est très proche de l'incidence de Cz zéro.
`Ra` est faible.
`Ft` est < 0.
`Fr` est > 0.
Fonctionnement reverse
`α` est très négatif car ` θ` est inférieur à 0. Dans ce cas l'hélice ne travaillera jamais en moulinet.
`Ft` est < 0.
`Fr` est > 0.
Récapitulatif
Récapitulation des divers modes de fonctionnement sur la polaire de Lilienthal d'une section de pale.
À noter que les fonctions de propulsion, frein et moulinet sont possibles pour une hélice à calage fixe.
Les différentes hélices
Rendement d'une hélice
Nous avons vu dans GMP Courbes Wu/WN :
- `Wm` = Puissance moteur
- `Wu` = Puissance utile
- `η h` = Rendement de l'hélice
soit : `η h = \frac{Wu}{Wn}`
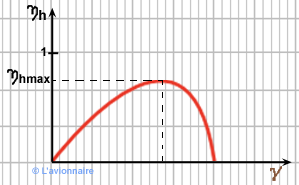
Le rendement maximal d'une hélice est de l'ordre de 0,8 à 0,85.
La courbe de rendement d'une hélice `η h` est établie en fonction de `γ` paramètre de fonctionnement de l'hélice.
soit : `γ =\frac{Va}{nd}`
- `Va` = Vitesse avion
- `n` = nombre de tours/s de l'hélice
- `d` = diamètre de l'hélice
Pas constant
Ce serait une hélice dont le pas resterait constant en toutes ses sections. Or une hélice est construite de manière qu'en utilisation normale l'incidence soit toujours égale à l'incidence de finesse max :
incidence de `ƒmax`= `θ - β`
Malheureusement, il est impossible de satisfaire à la fois :
- l'incidence de finesse max tout au long de la pale
- le pas constant tout au long de la pale
C'est pour cette raison que le pas n'est pas tout à fait constant le long de la pale et que H varie d'une section à l'autre.
Dans une hélice à pas constant, le calage diminue du moyeu à l'extrémité de la pale.
Nombre de pales et diamètre
Les hélices peuvent être bipale, tripale, quadripale voire plus, comme l'Airbus A 400M avec huit pales.
À noter que le rendement max sera obtenu par une hélice bipale. Par contre une hélice tripale ou quadripale aura un encombrement (diamètre) plus faible avec une vitesse en bout de pale inférieure à la bipale.
Vitesse en bout de pale
Pour une hélice de 1,80 m soit un rayon de 0,90 m et une vitesse de 2400 tours/minute ou 40 tours/seconde, la vitesse en bout de pale sera égale au demi diamètre de l'hélice multiplié par 2 pi et multiplié par les tours/seconde :
Soit : 0,90 * 2π * 40 = 226,10 m/s ou 813,88 Km/h.
À cela, il faut maintenant combiner cette vitesse avec celle de l'avion.
Si X est la vitesse de l'avion et Y la vitesse de rotation en bout de pale, nous aurons en Z la vitesse réelle du bout de pale.
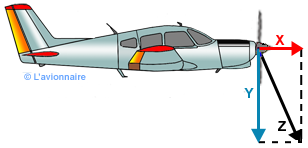
Soit : `Z^2 = X^2+Y^2`
Si la vitesse de l'avion est de 360 km/ soit 100 m/s nous aurons :
`V^2= 100^2 + 226,1^2 = 10000 + 51121,21 = 6112,21`
et `V = \sqrt{6112,21}` = 247,22 m/s = 890 km/h .
La vitesse du bout de pale est de 890 km/h pour une vitesse avion de 360 km/h.
Pour éviter le bruit et une baisse de rendement, la vitesse maximale en bout d'une pale est limitée à environ 85 % de la vitesse du son (Mach 1 = 340 m/s dans l'air à 15 °C) soit 290m/s. C'est pour ces raisons que le diamètre d'une hélice et sa vitesse de rotation sont limités.
Une hélice de 1,80 m à 3600 tours/min atteindra cette limite. D'où la nécessité d'un réducteur entre le moteur et l'hélice, si la vitesse de rotation du moteur est importante. Les avions turbopropulseurs sont tous équipés d'un réducteur. Voir Les turbopropulseurs
Les différents calages
Hélice à calage fixe
Les premières hélices étaient à pas fixe. Actuellement, les avions légers dans les aéro-clubs sont encore équipés d'hélices à pas fixe. Le petit pas permet des montées rapides (cas des avions remorqueurs) et des évolutions en voltige. Les avions de voyage sont équipés d'une hélice grand pas, les performances de montée n'étant pas la priorité.
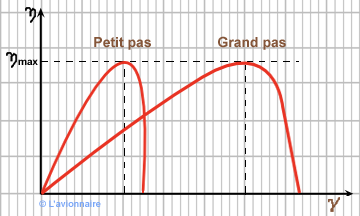
Petit pas :le paramètre de fonctionnement `γ` est faible.
Grand pas : le paramètre de fonctionnement `γ` est fort.
Hélice à calage variable
C'est la possibilité de modifier l'angle de calage `θ` par rotation autour de l'axe de la pale.
- Au décollage : `V` est faible, `η` est élevé, donc `γ` est faible. Pour avoir un rendement optimum, il faut que `h` soit petit.
- En croisière : `V ` est élevée, `η` est moyen, donc `γ` est élevé et pour avoir toujours le rendement optimum, il faut que ` h` soit grand.

Exemple :
Nous savons que : `h = 2,2 tan θ` (voir Pas relatif)
Soit une hélice dont le calage à `0.7 R` varie de 18° à 32°
nous aurons :
`θ` = 18° `tan θ` = 0,325 `h ` = 0,715
`θ` = 32° `tan θ` = 0,625 `h ` = 1,375
Hélice à régime constant
Pour qu'un moteur fonctionne de façon optimale, il faut en général que le nombre de tours n soit constant.
On obtient n constant, quelles que soient V et Wm en utilisant un régulateur d'hélice.
Sur le dessin ci-dessous, le régime fonctionne au point A pour un pas h1 à n max.
Si pour une raison extérieure V ou Wm croît, n augmente, mais le régulateur va agir de façon à maintenir n constant et h1 va croître. L'hélice fonctionnera alors avec un nouveau pas h2 au point B et un nouveau `γ`
En règle générale, le régulateur adoptera un pas pour que l'hélice reste très proche du rendement maximal. Point C ci-dessous.
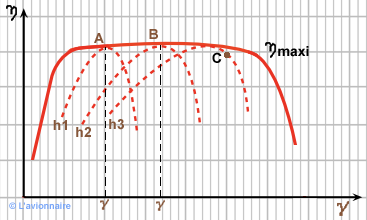
Afin d'éviter toute détérioration, un régulateur d'hélice fait varier le pas entre deux butées.
Exemple : Sur Fokker 27 utilisé longtemps dans les compagnies aériennes et notamment françaises,
la butée de décollage était de 18° et la butée de croisière à 32.
Hélice nouvelle génération
La technologie a progressé au cours des années jusqu'à l'utilisation actuelle de pales en composite, ainsi que de commandes d'hélice électroniques.
L’hélice de l’avion de transport Airbus A400M avec ses 8 pales pour un diamètre de 5,3 m développe une puissance de 10 700 CV.

Hélice en cours d'étude
Une ou deux hélices transsoniques contrarotatives entrainées par une ou deux turbines libres tournant en sens inverse. Grâce à un rendement de propulsion pouvant atteindre 0,85 à Mach 0,8, la consommation de kérosène pourrait diminuer de 20 à 25 %. Ces hautes performances sont dues à leur profil supercritique et à leurs formes.
Mais ce concept ne sera pas prêt avant 2020 à 2025.
Ci-dessous, un moteur open rotor à deux soufflantes contrarotatives appelées également Propfans.


