
RADARS MÉTÉOROLOGIQUES AÉROPORTÉS
UN PEU DE MATHS
La source de cette page provient de Radiotutorial.eu édité par Christian Wolff et Pierre Vaillant, version septembre 2011.
Introduction
Les radars météorologiques modernes utilisent des techniques sophistiquées pour transformer le signal brut et en tirer la donnée météorologique. Ils utilisent diverses informations contenues dans le signal de retour : réflectivité, vitesse Doppler et signal à double polarimétrie.
Équation radar pour cibles volumiques
L’équation qui permet de calculer la puissance retournée à un radar météorologique par les hydrométéores est une variation de l’équation du radar d’un radar primaire :
| `Pc=frac (Ps.G^2.\lamda^2.\sigma)( (4\pi)^3 .R ^4 ` |
Où Pe = Puissance retournée au radar Ps = Puissance émise G = Gain de l'antenne σ = surface équivalente radar λ = Longueur d'onde du radar R = distance des cibles |
Surface équivalente volumique
| La différence tient au fait que le faisceau frappe une multitude de gouttes dans chaque cellule de résolution, ce qui modifie l’expression de σ. La grosseur des gouttes rencontrées dans la pluie est beaucoup plus petite que la longueur d’onde du radar et, par conséquent, l’équation de Rayleigh pour la rétrodiffusion d’une goutte devient : |
 |
| `σ_i=frac (\pi^5)( \lamda^4)|K|^2D_i^6` et `|K|^2 =|frac (\epsilon -1)( \epsilon +2)|^2` |
où D est le diamètre des gouttes et ε la permittivité ou constante diélectrique. |
Pour un radar de bande L à X , `|K|^2` = 0.93 pour l’eau et `|K|^2`= 0.2 pour la glace.
En faisant la somme de toutes les gouttes dans 1 m3, nous obtenons `η`, la réflectivité radar par unité de volume :
| `η= frac (\pi^5)( \lamda^4)|K|^(2.)Z; Z = \sum_(i=1)^n D_i^6` |
où Z est la réflectivité totale du radar |
Effets de D et K
En substituant la réflectivité d’une nuée de gouttes à σ d’une cible unique, nous avons introduit deux paramètres qui peuvent faire varier grandement le retour au radar:
- le diamètre D des gouttes de pluie est bien différent de celui de la bruine ou des flocons de neige. Même à l’intérieur de la pluie, les gouttes n’ont pas toutes la même grosseur. Comme, D est à la 6ième puissance, une seule grosse goutte a plus d’effet sur la réflectivité qu’une multitude de petites. Une goutte de 5 mm a la même réflectivité que 56 gouttes de 1 mm.
- K étant différent pour l’eau et la glace, l’intensité du signal de la pluie sera plus grande que celle des cristaux de glace pour un même diamètre. Cependant, les flocons de neige, qui sont formés de cristaux, sont en général plus gros que les gouttes de pluie.
Effets sur l'équation radar
| L’équation du radar peut être réécrite en tenant compte du fait que `η` est remplacé par η multiplié par le volume sondé. Quand la pluie remplit le faisceau, le volume sondé est : `V = frac (\pi^.\ θ^.\ϕ^.R^(2.)C_0^.\τ)(8)` |
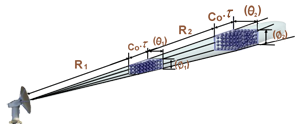 |
Le volume est lui-même proportionnel à la distance au radar selon la définition de la cellule de résolution du radar dans le dessin ci-dessus. On peut remplacer les valeurs de `σ` et du volume pour obtenir :
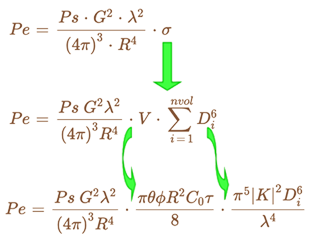
Le volume de la cellule de résolution augmente comme le carré de la distance. Une telle cellule est remplie de gouttes qui rétrodiffusent de l’énergie vers le radar. Contrairement à un avion qui renvoie un signal ponctuel, l’énergie de toutes les gouttes dans le volume s’additionne. En simplifiant les termes de la nouvelle équation ci-dessus, on obtient que :
| `Pe= kPs cdot (frac(\epsilon)( \lamda^4 cdot R^2))sum ND^6` |
Où : Pe= Puissance retournée au radar Ps = Puissance émise k = constante du radar λ = Longueur d'onde du radar ε = est la permittivité ou constante diélectique N = Nombre de gouttes avec diamètre D D = Diammètre des gouttes |
Réflectivité
La réflectivité Z est la puissance retournée à un radar météorologique quand le faisceau rencontre des hydrométéores (pluie, neige, etc.). Il est défini par la surface équivalente radar `σ` par mètre cube pour de petites sphères ayant une permittivité, ou constante diélectrique, non nulle. Cette valeur varie comme la 6ième puissance du diamètre d’une sphère de diamètre D. Comme chaque goutte ou flocon a un diamètre différent, la réflectivité est donc la somme de la réflectivité individuelle de toutes les gouttes ou flocons, ce qui donne :
`Z = \int_(0)^(Dmax)N_(0)e ^(-AD) D^6 dD `
La variation de diamètre et la constante diélectrique entre les différents types de précipitations (pluie, neige, bruine, grêle, etc.) est très grande et la réflectivité équivalente est donc exprimée en dBZ (10 fois le logarithme du rapport ou décibel Z).


