
INSTRUMENTS DE VOL
MESURE DE L'ALTITUDE
Introduction
En aéronautique, un certain nombre de paramètres sont normalisés.
Ainsi, on considère qu'au niveau de la mer :
- la pression est P0 = 1 013,25 hPa,
- la température est T0 = 15 °C = 288,15 K,
- la densité de l'air est ρ0 = 1,225 kg/m3 = 35,537 64 g/ft3,
- la pesanteur est g0 = 9,807 m/s2 = 32,174 ft/s2,
- la vitesse du son est a0 = 1 225,059 68 km/h = 340,294 36 m/s = 661,479 31 kt,
- l'humidité est h0 = 0 %.
L'altimétrie est la détermination et la mesure des altitudes d'un lieu ou d'une région donnée. Elle est également la technique qui permet de calculer avec le moins d'erreurs possibles, l'altitude d'un aéronef.
L'état de l'air peut être défini par trois paramètres :
- pression statique ou pression atmosphérique Ps ;
- masse volumique ρ ;
- température statique ou température ambiante θ ;
Mais l'air est un milieu extrêmement changeant, aussi a-t-il été nécessaire de fixer les relations reliant ces paramètres et l'altitude, de façon à définir une atmosphère de référence appelée
Atmosphère standard.
Atmosphère standard
L'atmosphère standard est dans la majorité des cas, différente de l'atmosphère réelle.
Elle est définie à partir des relations suivantes, l'air étant considéré "calme" (vent nul) :
`dPs = - ρ g d Z ` ( statique des fluides ; `g` = accélération de la pesanteur = 9,8066 m/s2)
`\frac{Ps}{ρ} = r T` air considéré comme gaz parfait ; `r = \frac{287 J }{°K}` et `T = (θ + 273) °K)`.
- Décroissance de pression dans les basses couches de 28 ft/hPa ;
- Décroissance verticale de la température de 6,5°C / 1000 m ou 2°C / 1000 ft) ;
- Température constante de - 56,6°C au-dessus de la tropopause.
Modélisation simplifiée dans la troposphère entre 0 et 11 Km d'altitude.
Définition des altitudes
L'état de l'air est défini par les 3 paramètres `Ps`, `ρ` ou `δ` et `Θ`. Ces paramètres étant fonction de Z, il est donc possible de mesurer l'altitude à bord des avions à l'aide d'un instrument sensible à l'un de ces trois paramètres.
Ceci conduit à la définition de trois altitudes. Ainsi, les performances d'un avion ou d'un moteur peuvent, au lieu d'être exprimées en fonction de la pression ou de la densité, ou de la température, être exprimées en fonction de l'altitude. Mais cela n'a de sens qu'en atmosphère standard. Donc, si en atmosphère réelle on veut dissocier l'influence des deux variables tout en conservant le terme altitude, il faut préciser "altitude-pression", ou "altitude-densité", ou "altitude-température".
Altitude-pression
L'altitude-pression en un point d'altitude réelle Z est l'altitude Zp qui correspond en atmosphère type à la pression Ps régnant en ce point. L'altitude-pression est l'altitude déduite en ne prenant que la pression statique entourant l'aéronef comme paramètre.
L'altitude-pression peut donc être directement lue dans un tableau d'atmosphère standard en face de la pression Ps régnant au point considéré.

Entre 0 et 11 Km d'altitude, l'altitude pression peut être donnée par la formule suivante :
- `Z` est l'altitude pression,
- `Ps` est la pression statique.
- `δT` gradient thermique adiabatique est constant et vaut −6,5 °C/km.
Si on est en atmosphère standard, l'altitude-pression est égale à l'altitude géopotentielle.
Si `Ps` est exprimée en « hPa » et `Z` est exprimée en « ft », la formule approchée est :
Altitude-densité
L'altitude-densité en un point d'altitude réelle Z est l'altitude Zd qui correspond en atmosphère type à la densité relative `δ` régnant en ce point. Donc l'altitude densité est l'altitude d'un lieu pour lequel la densité réelle serait égale à la densité théorique en atmosphère standard (ce qui n'est jamais le cas dans le monde réel).
Il est évident que si l'atmosphère réelle est identique à l'atmosphère-type Zp = Zd.
L'altitude-densité est donc d'altitude-pression corrigée de la différence de température entre :
-` Θr` : température réelle à `Zp`
- `Θ ` : température standard à `Zp`

Entre 0 et 11 Km d'altitude, l'altitude densité peut être donnée par la formule suivante :
- `DA` est l'altitude densité,
- `Ps`> est la pression statique,
- `Ts` est la température statique.
Les autres paramètres sont décrits dans la section quelques paramètres en début de page.
Si on considère que `Ps` est exprimée en « hPa », `Ts` est exprimée en « °C » et `DA` est exprimée en « ft », la formule approchée est :
Différents calculs de Zd
|
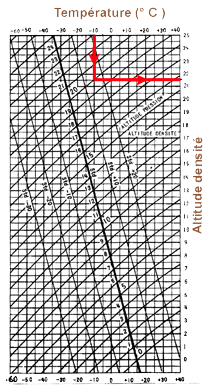
Zd peut être obtenue : 1) à l'aide d'un abaque ci-contre - Zp 20 000 ft - Θr = - 10 °C Zd = 21 600 ft 2) à l'aide d'un computeur - Zp 20 000 ft - Θr = - 10 °C Zd = 21 700 ft 3) à l'aide d'une formule approchée suivante : - en mètres Zd = Zp = + 36 (Θr - Θ en °C) - en ft Zd = Zp = + 120 (Θr - Θ en °C) |
 |
Altitude-température
L'altitude-pression en un point d'altitude réelle Z est l'altitude Zp qui correspond en atmosphère type à la pression Ps régnant en ce point.
L'altitude-pression peut donc être directement lue dans un tableau d'atmosphère standard en face de la pression Ps régnant au point considéré.

Effet de la pression et de la température sur l'altitude
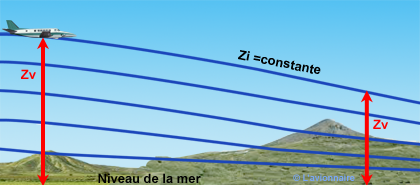
L’altimètre est conçu selon les principes de l’atmosphère standard. Donc, lorsqu'un avion vole à une altitude constante indiquée par un altimètre réglé par exemple à 1013,2 hPa (niveau de vol), il suit la surface isobarique 1013,2 hPA. Si l'altitude réelle de cette surface isobare diminue, l'altitude vraie de l'avion diminue également. C'est le cas d'un avion volant d’une zone anticyclonique (Haute Pression) vers une zone dépressionnaire (Basse Pression).
- Vers une dépression : si Zi est constant, alors Zv diminue
- Vers de basses températures : si Zi est constant, alors Zv diminue
D'ou la régle des 4 D :
Dépression = Dérive Droite = Danger

