
LES TURBOMACHINES
UN PEU DE MATHS
Introduction
Le turboréacteur répond aux deux principes de la thermodynamique :
- le premier, appelé principe de l'énergie, qui s'applique à un système évoluant d'un état initial vers un état final avec conservation de la masse. Le changement d'état de ce système prend en compte les échanges avec l'extérieur sous forme de Travail ou de Chaleur. L'énergie par unité de masse d'un système gazeux est appelée enthalpie et l'énergie fournie sous forme de travail ou de chaleur par le générateur de gaz du turboréacteur est proportionnelle au débit masse du fluide traversant la machine et à la variation d'enthalpie que subit ce fluide.
- le deuxième, basée sur la notion d'entropie ou d'énergie utilisable, met en évidence l'irréversibilité de la transformation et donc de la perte d'énergie que subit le fluide en traversant la machine.
Le cycle d'un turboréacteur est constitué d'une compression adiabatique réversible, d'une combustion isobare irréversible (le réacteur étant considéré comme un système ouvert), d'une détente adiabatique réversible et d'un refroidissement isobare réversible.
Les sources de cette page proviennent de fr.Wikipedia.org.
Cycle thermodynamique
Le cycle thermodynamique du turboréacteur comprend quatre stades où l'air subit des modifications physiques ou chimiques :
1 - aspiration ;
2 -compression ;
3 -combustion ;
4 -détente / éjection.
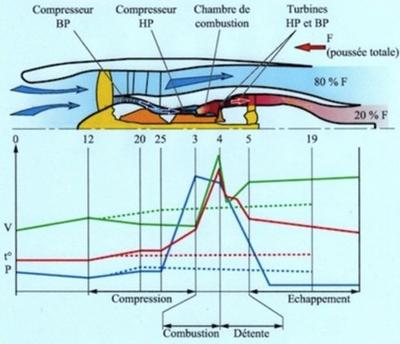
Ces quatre phases du cycle thermodynamique s'effectuent simultanément à des endroits différents par opposition aux quatre temps du moteur à explosion qui se réalisent au même endroit (dans le même cylindre) et à des instants différents.
Pour assurer la réalisation de ce cycle, le turboréacteur (mono flux) est constitué de deux parties :
un ensemble compresseur-foyer-turbine qui transforme l'énergie chimique du carburant en énergie potentielle de gaz comprimés et chauds ; une tuyère d'éjection qui transforme en vitesse l'énergie de pression fournie par le générateur de gaz.
Répartition des forces de poussée
La poussée, qui est la performance essentielle d'un propulseur fournissant de l'énergie cinétique, est une force en réaction à l'accélération d'une masse d'air le traversant.
Les efforts principaux se répartissent ainsi :
- 60 % vers l'avant pour la force de réaction du compresseur ;
- 30 % vers l'avant pour la force de réaction en provenance de la chambre de combustion ;
- 10 % vers l'avant pour la force de réaction de l'arbre ;
- 55 % vers l'arrière pour la force de réaction de la turbine.
Cela donne une poussée effective (force vers l'avant) de 45 % de la force totale.
Calcul de la poussée
La poussée peut se calculer en mesurant le débit d'air et les vitesses d'entrée d'air et de sortie des gaz, car comme dans tous les moteurs à réaction directe, elle résulte principalement de deux causes :
1 - la différence de quantité de mouvement entre l'air admis et les gaz éjectés pendant l'unité de temps ;
2 - la force résultant de la différence de pression existant entre la sortie de la tuyère et l'infini amont.
La poussée d'un turboréacteur est donc :
1 - proportionnelle, en négligeant la masse de carburant injectée, au débit-masse d'air le traversant ;
2 - une fonction croissante de la vitesse d'éjection des gaz en sortie de tuyère.
Soit :
`F` : Poussée du turboréacteur
`D` : Débit massique de l'air traversant le turboréacteur
`V_1` : Vitesse air de l'avion
`V_2`: Vitesse d'éjection des gaz en sortie de tuyère
`S_1` : Section d'entrée d'air du turboréacteur
`S_2` : Section de la tuyère en sortie
`P_0` : Pression ambiante à l'infini amont
`P_2` : Pression statique à la sortie de la tuyère
La différence des quantités de mouvement s'écrit, en négligeant la masse de combustible injecté :
La différence des pressions entre la sortie de tuyère et l'infini amont conduit à écrire :
d'où l'expression de la poussée :
Le terme `(P_2\times S_2-P_0\times S_1)` est suffisamment petit pour être négligé et l'expression réduite de la poussée peut s'exprimer à partir des équations:
1 - En vol : `F=D(V_2-V_1)`
2 - Au sol au point fixe : `F=D(V_2)`
La mise en vitesse des gaz se fait dans la tuyère par transformation de l'énergie potentielle de pression totale et de température totale en énergie cinétique à la sortie du col de tuyère. Tant que la tuyère est en régime subsonique, la pression statique dans le plan de sortie est égale à la pression ambiante. Si la vitesse des gaz devient supérieure à Mach 1 alors la pression statique au col devient supérieure à la pression ambiante et des ondes de choc se forment en aval (anneaux en sortie de tuyère sur réacteurs en post-combustion).
La vitesse isentropique en sortie de tuyère a pour équation :
avec :
`γ` : Rapport des chaleurs massiques à pression et volume constant.
Ainsi, pour que le turboréacteur crée une poussée vers l'avant, il faut que la vitesse des gaz d'échappement soit supérieure à celle de l'aéronef.
Une même poussée peut être obtenue avec un débit plus faible et une vitesse d'éjection du gaz plus élevée, ou au contraire, un débit plus élevé à moindre vitesse. Il est cependant plus avantageux de favoriser le débit plutôt que la vitesse dans le cas des vitesses subsoniques.
Puissances et rendements
Il faut distinguer plusieurs niveaux de puissance et donc de rendement dans le fonctionnement du turboréacteur :
La puissance calorifique fournie au turboréacteur à partir de la combustion d'un carburant et qui s'exprime par le produit du débit carburant et de son pouvoir calorifique. C'est la puissance que l'on pourrait extraire du carburant si la machine était parfaite et qui s'exprime par la formule :
avec :
- ` Wς` : puissance fournie par le carburant
- `η_t`: rendement théorique du cycle
La puissance thermique communiquée à la masse gazeuse pendant son passage dans la machine et qui s'exprime par la formule :
La puissance cinétique du jet de gaz éjecté à la sortie de la tuyère et qui s'exprime par la formule :
La puissance propulsive qui est la puissance prélevée sur la puissance cinétique des gaz éjectés que l'avion utilise réellement et qui est le produit de la poussée par la "vitesse air" de l'avion
À partir de ces niveaux de puissance on détermine plusieurs niveaux de rendement pour le turboréacteur :
Le rendement thermodynamique (40 %) qui est le rapport de la puissance thermodynamique à l'énergie fournie par le carburant et qui s'exprime par la formule :
Ce rendement caractérise l'efficacité de la machine à produire de l'énergie potentiellement utilisable pour la propulsion. On améliore ce rendement en augmentant la température du flux sortant de la chambre de combustion en corrélation avec l'augmentation du rapport de compression de l'air en amont de celle-ci. La réduction des pertes de charge et l'augmentation du rendement de l'ensemble turbine participe également à l'augmentation globale de ce rendement.
Le rendement interne (80 %) qui est le rapport de la puissance thermique à la puissance thermodynamique et qui s'exprime par la formule :
Le rendement propulsif qui est le rapport entre la puissance utilisée pour la propulsion et la puissance cinétique du jet (60 % pour une Vi donnée) caractérise la manière dont l'énergie produite par le générateur de gaz est réellement utilisée pour la propulsion. on améliore ce rendement en diminuant la vitesse d'éjection du jet pour l'adapter aux performances de vitesse attendues de l'avion.
Le rendement global (20 % à 25 %) qui est le rapport de l'énergie produite à l'énergie libérée par le carburant et qui peut s'exprimer par la formule :

