
MÉCANIQUE DU VOL
GMP VOL EN DESCENTE
- Influence de Wu
- Influence de l'altitude
- Influence du poids mg
- Influence du vent
- Influence des volets
Équation du vol en descente
Nous avons :
- `Ø` assiette est l'angle formé entre l'axe du fuselage et l'horizontale ;
- `γ` la pente est l'angle formé entre l'horizontale et l'axe des vitesses.
- `α` l'incidence est l'angle formé entre l'axe longitudinal de l'avion et la direction du vent relatif (axe des vitesses).

Rappelons que nous ferons les hypothèses suivantes :
- le vol est symétrique.
- le centre de poussée et le centre de gravité sont confondus.
- le vecteur vitesse est constant.
- l'angle de calage de la voilure est = 0 ( `α` avion = ` α` profil).
- L'incidence `α` est négligeable devant la pente
` γ` d'où `Ø` = ` γ`
Comme en vol horizontal, trois grandes forces s'exercent sur un aéronef en descente :
- Le poids `\vec{mg}`
- La traction `\vec{Tu}`
- La résultante aérodynamique `\vec{Ra}`
Le mouvement étant rectiligne uniforme : `\vec{Ra}+\vec{Tu}+\vec{mg}= \vec{0}`
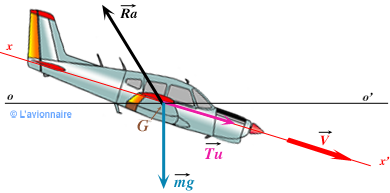
Ces trois grandes forces se décomposent suivant deux axes :
- L'axe de sustentation z z' toujours perpendiculaire au vecteur vitesse.
- L'axe de propulsion x x' toujours parallèle au vecteur vitesse.
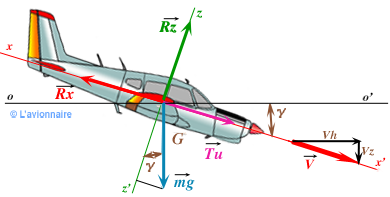
Les équations de vol en descente deviennent :
Équation de sustentation : ` mg cos γ = Rz`
Équation de propulsion: `Tu + mg sin γ = Rx`
Équation de finesse: `Cz = ƒ (Cx)`
En descente rectiligne uniforme la composante `mg sin γ` vient s'ajouter à la traction `Tu` pour compenser la traînée.
Si la traction est nulle, cas du planeur nous aurons :
Équation de sustentation : ` mg cos γ = Rz`
Équation de propulsion : `mg sin γ = Rx`
Vitesse verticale Vz
En multipliant par V nous pouvons transformer l'équation de puissance en :
- `Rx \times V` représente la puissance nécessaire au vol horizontal à la vitesse `V` .
- `Tu \times V ` représente la puissance nécessaire pour descendre.
- ` mg \times V sin γ` est la puissance qu'il faut retirer au vol horizontal si l'on veut descendre à la même vitesse.
Ce qui donne :
` ΔW` étant le manque de puissance.
Si `Tu = 0`, `Wu = 0` (cas du planeur) `Vz =\frac{Wn}{mg}`
La vitesse de vol `Vv peut se décomposer en une vitesse horizontale et une vitesse verticale `Vz`
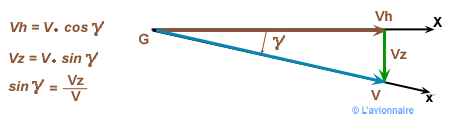
Pente de descente
Or comme en montée les `Vz` ont une valeur faible par rapport à la vitesse propre, on peut donc considérer que :
`\frac{Vz}{V} ` = pente en % = `sin γ ` = `γ radian` et si ` γ` faible =` \frac{Tn - Tu}{mg}`
Une pente de 5 % est égale à une pente de 0,05 radian .
Et le calcul simplifié est :
Attention : Pour que la formule soit correcte, il faut utiliser pour les Vz les pieds ft (feet) par minutes et pour les vitesses les noeuds Kt (Knot).
Influence de Wu sur le vol en descente
La `Vz \text{mini}` correspond également à l'incidence du point B c'est à dire à l'incidence de : `\frac{Cx}{Cz\frac{3}{2}}\text{minimal}`
Et l'angle de `γ \text{mini}` (pente) correspond à une incidence inférieure.
Si nous diminuons `Wu` la `Vz \text{mini}` correspond toujours au point B : `\frac{Cx}{Cz\frac{3}{2}}\text{minimal}`
Mais le lieu de `γ \text {mini}` change.
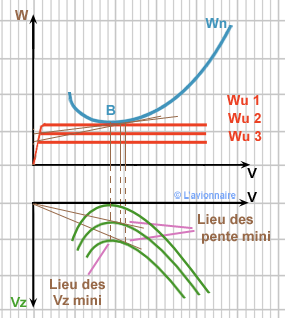
Note : Si tous les moteurs sont arrêtés, la vitesse de la pente minimale sera obtenue pour l'incidence de finesse maximale (cas du planeur).
Influence de l'altitude sur le vol en descente
Lorsque `Z` augmente , les courbes `Wn (V)` se déduisent par une homothétie de centre 0 de rapport : `\frac{1}{\sqrt {∂}`
Nous savons que `Wu` reste constant jusqu'à l'altitude de rétablissement puis diminue ensuite.
GMP Courbes Wu/Wn
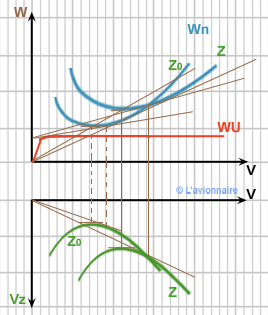
Dans ce cas lorsque `Z` diminue :
- `Vz \text {mini}` diminue.
- `γ \text {mini}` diminue.
- Les vitesses diminuent.
Mais l'incidence de `Vz \text {mini}` reste la même.
Pour une descente à un taux imposé, il suffit d'ajuster la `Wu` afin de conserver la `Vz` désirée .
Influence du poids mg sur le vol en descente
Nous supposerons que la descente se fait moteurs pleins réduits.
La `Vz` est proportionnelle à `\sqrt mg` . Donc à incidence constante, la `Vz` diminue lorsque le poids `mg` diminue et la vitesse sera plus faible.
La pente mini reste inchangée car elle ne dépend pas de `mg` : angle d'incidence de la finesse max
Influence du vent sur le vol en descente
Influence du vent sur la descente franchissable maximale.
Vent de face

- La pente `γ` minimale est plus forte que par vent effectif nul. L'incidence pour tenir cette pente est plus faible, mais la vitesse est plus forte.
- La `Vz` reste inchangée.
Vent arrière
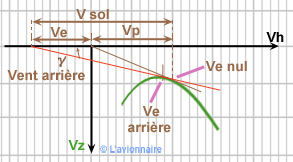
- La pente `γ` minimale est plus faible que par vent effectif nul. L'incidence pour tenir cette pente est plus grande, mais la vitesse est plus faible.
- La `Vz` reste inchangée.
Influence des volets hypersustentateurs sur le vol en descente
En descente moteurs complètement réduits à la même incidence :
- La `Vz \text {mini}` reste constante pour un faible braquage puis augmente pour des forts braquages.
- La `\text{pente mini}` augmente avec le braquage.
- La vitesse sera plus faible avec les volets braqués.

