
AÉRODYNAMIQUE
L'AIR EST UN FLUIDE
- L'air constituant l'atmosphère
- Loi de continuité du débit-masse
- Théorème de Bernoulli
Loi des gaz parfaits
Le gaz parfait est un modèle thermodynamique décrivant le comportement des gaz réels à basse pression.
Sur les plans macroscopiques, on appelle gaz parfait tout gaz vérifiant simultanément :
loi de Boyle-Mariotte
à température constante, le produit de la pression p par le volume V : pV est considéré comme constant lorsque la pression est faible ;
loi d'Avogadro
tous les gaz parfaits ont le même volume molaire dans les mêmes conditions de pression et de température.
loi de Gay-Lussac
à volume constant, la pression d'un gaz parfait est directement proportionnelle à la température absolue (exprimée en kelvins) ;
loi de Charles
à pression P constante, le volume d'un gaz parfait est directement proportionnel à la température absolue (exprimée en kelvins) ;
loi de Dalton
la pression totale exercée par un mélange de gaz est égale à la somme des pressions que chaque gaz exercerait s'il était seul.
Sur le plan microscopique, la théorie cinétique des gaz permet de retrouver ce comportement de gaz parfait : un gaz parfait est un gaz dont les molécules n'interagissent pas entre elles en dehors des chocs et dont la taille est négligeable par rapport à la distance intermoléculaire moyenne. L'énergie du gaz parfait est donc la somme de l'énergie cinétique du centre de masse des molécules et de l'énergie interne de chaque molécule (rotation, oscillation). Lorsque ces deux énergies sont proportionnelles, on a le Gaz parfait de Pierre-Simon de Laplace. Définition Wikipédia.
L'air constituant l'atmosphère
L'air est le mélange de gaz constituant l'atmosphère de la Terre.
L'air est un fluide compressible, c'est-à-dire que sa masse volumique ρ varie. Il est capable de s'écouler et de changer de forme.
La masse volumique (en kg/m3) est fonction de la pression, de la température et du taux d'humidité.
Pour de l'air sec sous pression atmosphérique normale :
- on prend généralement 1,293 kg/m3 à 0 °C et 1,204 kg/m3 à 20 °C.
La pression, qui est définie par une force par unité de surface, s'exprime en pascal Pa.
La pression de l'air diminue avec l'altitude.
Environ 101300 Pa, soit 1013 hPa ou 29,92 inHg au niveau de la mer (soit environ 1 bar).
La température s'exprime soit en degrés Kelvin (K), soit en degrés Celsius (C). Elle diminue avec l'altitude.
En pratique, on utilise surtout le degré Celsius qui ne constitue qu'une translation d'échelle :
- t°(C) = T(K) – 273,15.
La densité est le rapport entre la masse volumique à un niveau donné et la masse volumique standard au niveau de la mer.
D'autres grandeurs sont utiles telles que la viscosité (dans les considérations de traînée) et l'humidité (relative et absolue), en particulier dans la partie météorologie.
ISA International Standard Atmosphère
L' ISA permet de déterminer les performances de l'avion et est définie par les valeurs suivantes :
- Température : 15 °C (288 K) au niveau de la mer.
- Diminution de 2 °C / 1000 ft ) soit (0,65 °C / 100 m) jusqu'à 36 090 ft (11 000 m).
- Pression : 1013,25 hPa au niveau de la mer.
- Masse volumique : 1,225 kg/m3 au niveau de la mer.
Loi de continuité du débit-masse
Écoulement permanent
On appelle écoulement permanent un écoulement qui se reproduit identique à lui-même au cours du temps. Observé à un instant to, un écoulement permanent présentera les mêmes caractéristiques de vitesse, de pressions, etc... qu'à un instant t1 différent.
Trajectoire
La trajectoire est le lieu décrit par une particule fluide au cours du temps.
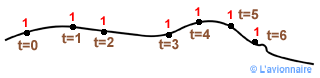
Ligne de courant
Plus délicate à saisir, la ligne de courant est une ligne définie à un instant donné par la tangente en chacun de ses points au vecteur vitesse en ce point.
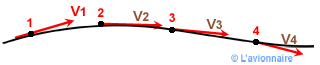
Trajectoires et lignes de courant sont fondamentalement différentes. L'une décrit le mouvement d'une molécule au cours du temps et l'autre décrit l'état du fluide à un instant donné.
Dans un écoulement permanent, la notion de temps n'ayant plus d'importance, les lignes de courant sont confondues avec les trajectoires.
Tube de courant
On appelle tube de courant un ensemble de lignes de courant traversant une surface arbitraire ds.
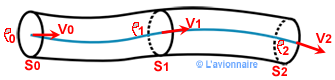
Quand l'écoulement est permanent, toutes les particules rentrant en S0 avec la vitesse V0 ressortent en S2 avec la vitesse V2 en passant par S1 avec la vitesse V1.
En effet, aucune particule ne sort du tube de courant puisque sa frontière est constituée de lignes de courant. La vitesse est en chaque point tangente à cette frontière et il n'y a pas de composante normale et, par conséquent, pas de débit.
D'autre part, il n'y a pas d'accumulation de masse, par conséquent le débit-masse en S0 et le même qu'en S1 et S2.
Ce débit-masse est le produit du débit-volume SV par la masse volumique ρ, donc d'une manière générale, dans un tube de courant en écoulement permanent, ρ SV = constante
Théorème de Bernoulli
Une bonne illustration de ce principe de Bernoulli est le tube de Venturi (du nom d’un physicien italien du XVIIIe siècle, Giovanni Battista Venturi). La quantité d’air qui passe à l’entrée, au col et à la sortie, est identique : le débit d’air est constant.
Représentation simplifiée du tube de Venturi.
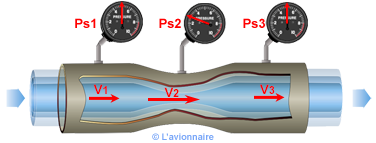
On observe que la vitesse varie : elle s’accroît lors du rétrécissement de section jusqu’au col et diminue lors de l’élargissement. Un fluide passant par un tel tuyau voit donc sa vitesse augmenter en même temps que sa pression diminue lors du rétrécissement au passage du col.
Nous avons : `Ps_1+\frac{1}{2}ρV_1^2= Ps_2+\frac{1}{2}ρV_2^2 = Ps_3+\frac{1}{2}ρV_3^2`
Le théorème de Bernoulli est une application de la conservation de l'énergie au cas des fluides en mouvement. Un certain travail est fourni au fluide lorsqu'il passe d'un point à un autre et ce travail est égal à la variation d'énergie mécanique.
Fluide laminaire visqueux et incompressible
On obtient la relation suivante :
`P_1+\frac{1}{2}ρV_1^2+ρgz_1= P_2+\frac{1}{2}ρV_2^2 +ρgz_2+Δp_(1,2)`
`P ` est la pression en un point (en Pa ou N/m²)
`ρ` est la masse volumique en un point (en kg/m³)
`V` est la vitesse du fluide en un point (en m/s)
` g` est l'accélération de la pesanteur (en N/kg ou m/s²)
`z` est l'altitude (en m)
`Δp_{1,2}` est la perte de charge et représente la densité d'énergie nécessaire pour qu'un fluide visqueux circule dans un tube.
Fluide parfait
Un fluide non visqueux est dit parfait, et dans ce cas `Δp_{1,2}=0`.
On obtient alors : `P+\frac{1}{2}ρV^2+ρgz =` constant
L'équation de Bernoulli
Hypothèses préalables :
- Le fluide est incompressible.
- Il s’écoule en régime permanent.
- Il n’est pas visqueux.
En plus, `ρgz` sera toujours négligé en aérodynamique du fait de la faible valeur de ρ pour l'air.
L'équation de Bernoulli s'écrit : `P+\frac{1}{2}ρV^2 =` constante
La constante s'appelle pression totale `Pt` c'est la pression que l'on aurait si l'on annulait la vitesse du fluide.
`\frac{1}{2} ρ V^2` est la pression dynamique `Pd`
Quant à ` P ` il s'agit de la pression statique ` Ps` c'est-à-dire la pression que l'on mesurerait si le fluide était au repos (vitesse nulle).
Soit : `Pt = Pd + Ps`
Donc lorsque `Pd` (pression dynamique) augmente, ` Ps` (pression statique) diminue.
Les souffleries aérodynamiques
Une soufflerie (en anglais wind tunnel) est une installation d'essais utilisée en aérodynamique pour étudier les effets d'un écoulement d'air sur un corps, généralement un modèle de dimension réduite par rapport au réel. En effet, il est essentiel de simuler le vol d’un avion avec la plus grande maquette possible pour visualiser l’écoulement de l’air, le plus souvent impossible à faire dans les conditions réelles de déplacement.
Il est nécessaire de rappeler qu’il n’existe pas une, mais des souffleries.
Souffleries à circuit ouvert
Ce type de soufflerie inventée par Gustave Eiffel fut construite en 1912 rue Boileau à Auteuil, elle est toujours en exploitation.
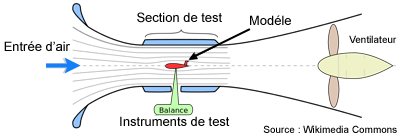
Souffleries à retour (en circuit fermé)
Source texte et dessins ONERA
Les souffleries continues :
La soufflerie sonique S1MA de l’ONERA à Modane est une soufflerie continue. C’est la plus puissante au monde, avec sa veine de 14 m de long et de 8 m de diamètre. Malgré ses grandes dimensions, la soufflerie est capable de monter jusqu’à la vitesse du son, soit Mach 1 (1200 km/h). Le débit d’air dans la section d’essai est alors de 10 tonnes d’air/seconde.
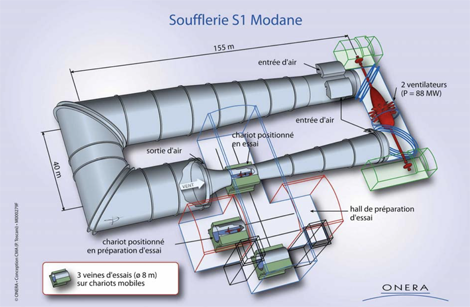
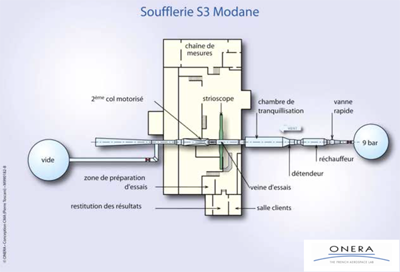
Les souffleries à rafales.
Les souffleries à rafales ne fonctionnent pas en circuit fermé, mais produisent des rafales d’une durée de quelques millisecondes à 15 minutes selon les conditions. La soufflerie S3 de Modane peut réaliser entre 3 et 20 rafales par jour.
L’air comprimé nécessaire aux souffleries à rafales de Modane (S3MA et S4MA) est produit sur place et stocké dans sept sphères, d’une capacité de 9 500 m3 à 9 bars et 3 réservoirs d’une capacité de 110 m3 à 270 bars (270 kg/cm2).
Cet air comprimé est éjecté soit dans l’atmosphère, soit dans des sphères à vide. Pendant l’essai, au travers d’un hublot en verre de 10 cm d’épaisseur, il est possible de visualiser les ondes de choc.
Si la soufflerie à rafales S3MA peut atteindre la vitesse d’un nombre de Mach égal à 5,5, la soufflerie S4 va encore plus loin, jusqu’à un nombre de Mach égal à 12.
Ci-dessous la maquette d'un Douglas MD 11 sur son support dans la chambre d'expérience.


