MÉCANIQUE DU VOL
GMP VOL HORIZONTAL
- Points caractéristiques
- Influence de l'altitude
- Influence du poids mg
- Influence des volets hypersustentateurs
Équation du vol horizontal
Nous avons :
- `Ø` assiette est l'angle formé entre l'axe du fuselage et l'horizontale ;
- `γ` la pente est l'angle formé entre l'horizontale et l'axe des vitesses. En vol horizontal `γ= Ø`;
- `α` l'incidence est l'angle formé entre l'axe longitudinal de l'avion et la direction du vent relatif (axe des vitesses).

Nous ferons les hypothèses suivantes :
- le vol est symétrique.
- le centre de poussée et le centre de gravité sont confondus.
- le vecteur vitesse est constant.
- l'angle de calage de la voilure est = ` 0 ` (`α` avion = `α` profil).
Les trois grandes forces qui s'exercent sur un aéronef en vol :
- Le poids `\vec{mg}`
- La traction `\vec{Tu}`
- La résultante aérodynamique `\vec{Ra}`
Le mouvement étant rectiligne uniforme : `\vec{Ra}+\vec{Tu}+\vec{mg}= \vec{0}`
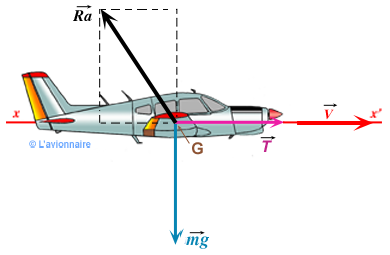
La résultante aérodynamique `\vec{Ra}` peut se décomposer en :
- `\vec{Rz}` = Portance ( force dirigée vers le haut ) est opposée a `\vec{mg}`
- `\vec{Rx}` = Traînée ( force opposée à l'avancement de l'aéronef ) est opposée `\vec{Tu}`
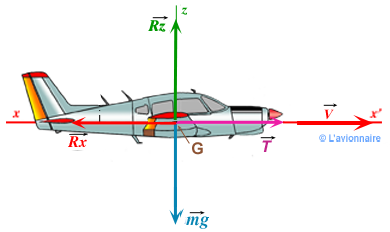
Nous avons:
Équation de sustentation : `mg= Rz=\frac{1}{2} ρSV^2Cz`
Équation de propulsion : `Tu= Rx=\frac{1}{2} ρSV^2Cx`
Équation de la polaire : `Cz = ƒ (Cx)`
`ρ` = masse volumique de l'air varie avec l'altitude
`S` = surface alaire de l'avion
`V` = la vitesse au carré
`Cz` = coefficient de portance
`Cx` = coefficient de traînée
Les régimes de vol
Portons sur un même graphique les courbes de `Wn` et `Wu` que nous avons étudié au paragraphe Courbes de puissance utile et puissance nécessaire.
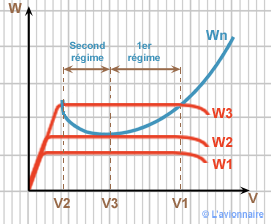
Nous avons trois cas possibles :
`Wu1` ne coupe jamais la courbe `Wn`. Le vol horiziontal est impossible à cette altitude, à cette température ou à cette masse pour cette `Wu`.
`Wu2` tangente `Wn`. Le vol horizontal est possible pour une seule vitesse `V3` donc à une seule incidence.
`Wu3` coupe la courbe `Wn` en deux endroits. En `V1` et en `V2`
`V1` vitesse la plus élevée avec une incidence faible.
`V2` vitesse la plus faible avec une incidence élevée.
Entre `V1` et `V3` nous sommes au 1er régime de vol.
Entre `V3` et ``V2 nous sommes au second régime de vol.
Le vol de croisière se fait toujours au premier régime, car à puissance égale donc à consommation de carburant égale la vitesse est plus élevée.
Stabilité et instabilité des régimes de vol
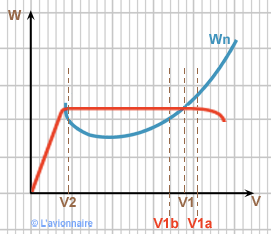
Stabilité du premier régime
Voyons pourquoi le 1er régime est appelé régime stable.
Supposons que pour une raison quelconque (turbulence, ascendance, etc.) la vitesse` V1` augmente et passe à `V1a`.
La puissance utile `Wu` étant inférieure à la puissance nécessaire `Wn`, la vitesse diminuera d'elle-même.
À l'inverse si la vitesse diminue et passe à `V1b`.
La puissance utile Wu étant supérieure à la puissance nécessaire `Wn`, la vitesse augmentera pour reprendre sa valeur d'avant la perturbation.
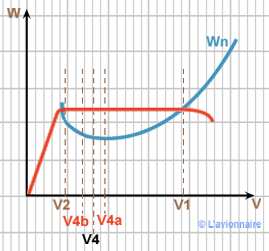
Instabilité du second régime
Voyons maintenant pourquoi le second régime est appelé régime instable.
Supposons que l'avion vole à une vitesse `V4` légèrement supérieure à la vitesse de décrochage.
Et que toujours pour une raison quelconque cette vitesse augmente et passe à `V4a`.
`Wu` étant supérieure à la puissance nécessaire `Wn` la vitesse continuera à augmenter.
À l'inverse si la vitesse diminue et passe à `V4b`, elle se rapproche dangereusement `V2`.
La puissance utile `Wu` étant inférieure à la puissance nécessaire `Wn`, la vitesse continuera à diminuer et la vitesse de décrochage sera rapidement atteinte.
Points caractéristiques de la courbe Wn
Trois points sont caractéristiques sur la courbe `Wn = f (V`)
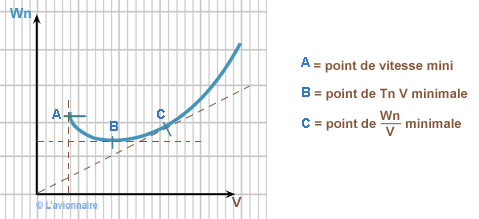
Vol à la vitesse minimale
La vitesse minimale nous est donnée par l'équation de sustentation.
Si `mg , S` et `ρ` sont fixés l'équation de sustentation est : `mg=\frac{1}{2} ρSV^2Cz`
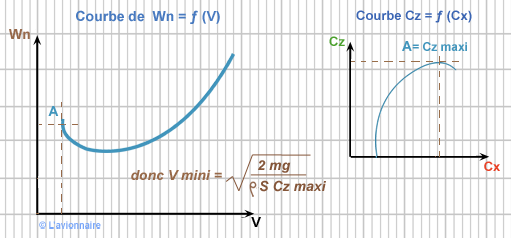
V sera mini pour Cz maxi et le point A sera le point de décrochage
Vol à la puissance minimale
Reprenons les équations du vol :
`P=\frac{1}{2} ρSV^2Cz`
`Wu=Wn =\frac{1}{2} ρSV^3Cx`
`Cx = ƒ (Cz)`
Cherchons le point de fonctionnement à la puissance minimale.
La courbe `Wn = ƒ(V)` étant graduée en incidence, la vitesse de vol à puissance minimale correspondra à une certaine incidence, donc à un `Cx` et à un `Cz` précis.
Eliminons `Vv` d'entre les équations de sustentation et de propulsion.
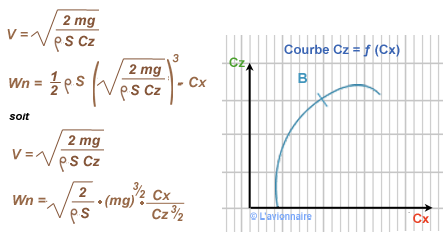
`mg`, `S` et `ρ` étant fixés `Wn` sera mini pour une incidence de `\frac{Cx}{Cz\frac{3}{2}}` minimal
Or il est impossible de repérer graphiquement sur la polaire ce point, il faudra donc construire une courbe spéciale.
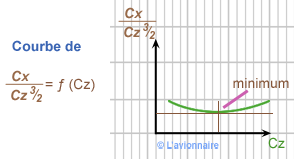
Ce point correspond à la puissance nécessaire minimale donc à la puissance utile minimale.
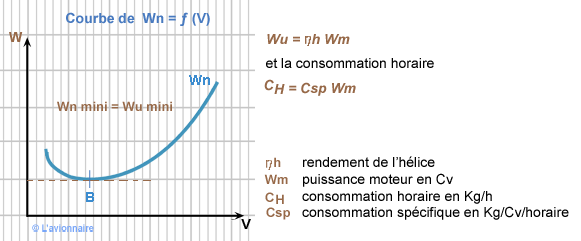
Le point B est le point de CH minimale et correspond au vol en attente.
Les unités utilisées sont celles couramment employées et non en MKSA
Vol à la finesse maximale
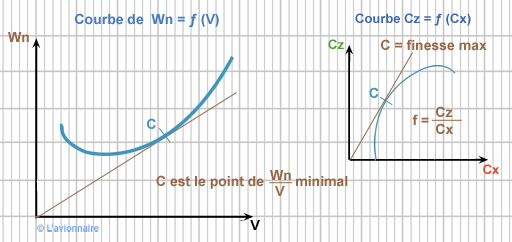
Nous avons: `\frac{Wn}{V} = mg\frac{Cx}{Cz}`
`mg ` étant donné le point C est le point de `\frac{Cx}{Cz} = \frac{1}{ƒ}\text{minimal}`
Le point C, est le point de finesse maximale.
Distance maximale franchissable
La consommation distance `Cd`
`Cd=\frac{CH}{Vs}` si `Ve` est nul nous aurons `Cd =\frac{CH}{Vp}`
alors
`Cd=\frac{CH}{Vp}= Csp\frac{Wn}{Vp}=\frac{Csp}{ηh}\times\frac{Wn}{Vp}`
`Csp` et `ηh` ne dépendent pas de la vitesse.
`Cd \text{mini}=Csp\frac{Wu}{V}\text{mini} = Csp\frac{Wn}{V}\text{mini}`
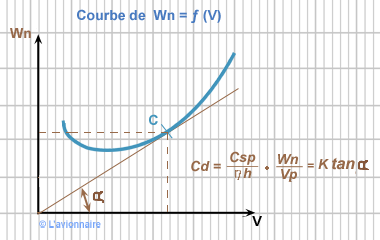
Le point C, est le point de distance franchissable appelé également point du Maxi-Range.
Maxi-range par vent non nul
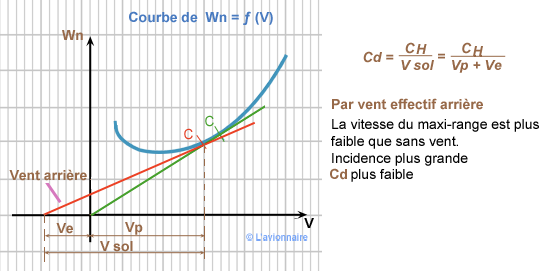
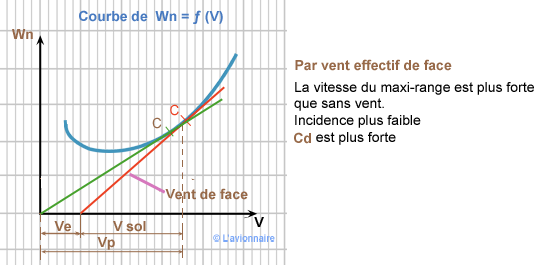
Nous pouvons donc indiquer sur la courbe `Wn = ƒ(V)` ces différentes zones.
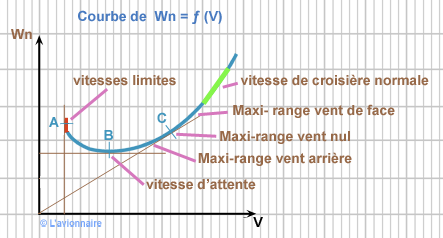
Vol de croisière
Dans le coût d'une heure de vol, il y a le prix du carburant, mais il y a également l'amortissement de la machine, le prix de revient de l'équipage, le coût de l'entretien, les assurances etc.
C'est pour toutes ces raisons que les vols de croisières se font toujours à des incidences inférieures à l'incidence de finesse maximale. Les consommations seront plus élevées qu'au maxi-range mais le vol sera quand même plus économique. Si l'autonomie de l'avion devait être juste pour effectuer un trajet, le choix se porterait alors sur le LONG RANGE.
Cd Long range = Cd maxi range + 1 % et la Vitesse Long range = Vitesse maxi range 4 à 5%.
ce qui permet d'être toujours du bon côté de la courbe même avec une imprécision dans la tenue des paramètres.
Influence de l'altitude
Influence sur Wn en = ƒ (V)
En considérant la masse de l'avion constante nous avons :
`V =\sqrt\frac{2mg}{ρSCz}` et `Wn =\sqrt\frac{2}{ρS}\times(mg)^\frac{3}{2}\times\frac{Cx}{Cz3/2}`
L'altitude intervient sous la forme d'une modification de la masse volumique.
Si à `Zo` nous avons `ρo` à `Z1` nous aurons : ` ρ = ρo∂`
En supposant que `Cz` et `Cx` reste inchangés donc à la même incidence nous aurons :
`V =\sqrt\frac{Vo}{∂}` et `Wn =\frac {Wno}{\sqrt ∂}`
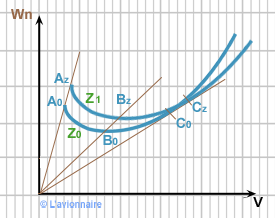
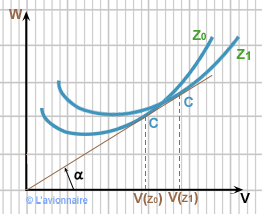
Les points iso-incidences des courbes `Wn = ƒ (V)` correspondant aux altitudes `Zo (ρo)` et `Z1 (ρ = ρo∂)` sont déduits par une homothétie de centre O et de rapport = ` \frac{1}\sqrt∂`
Les incidences sont des droites issues de l'origine.
Influence de l'altitude sur la consommation horaire
Nous avons : `Wu= Wn =\sqrt\frac{2}{ρS}\times(mg)^\frac{3}{2}\times\frac{Cx}{Cz3/2}`
`Wn` augmente si l'altitude augmente car ` ρ` diminue. Donc `Wu` augmente également.
Or `Csp ` (consommation spécifique) n'est pas constante en fonction de `Wu` , si `Wu` augmente `Csp` augmente.
`Csp` minimale correspondra à `Wn` mini soit
`\frac{Cx}{Cz3/2}\text{minimal}` et à l'altitude la plus basse possible, ou à l'altitude de rétablissement pour les avions munis d'un compresseur et d'un régulateur d'admission.
Influence de l'altitude sur le vol à la vitesse minimale
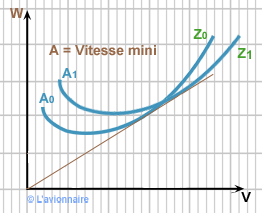
Ci-dessus nous constatons que le vol à vitesse minimale (vitesse propre), point A augmente avec l'altitude. La VC (vitesse corrigée) ou CAS (Calibrated Air Speed) reste la même. Donc la vitesse de décrochage lue sur l'anémomètre restera la même quelque soit l'altitude.
La Wn puissance nécessaire augmente également.
Influence de l'altitude sur le vol à la puissance minimale
`Wn = \frac{Wno}\sqrt ∂`
augmente lorsque `Z` augmente.
Comme la consommation horaire CH est fonction de la puissance, CH augmente lorsque Z augmente.
À une altitude plus ou moins élevée suivant que les moteurs sont équipés ou pas de compresseurs les courbes de puissance utile et de puissance nécessaire sont tangentes et l'avion a atteint son plafond de propulsion. Voir GMP vol en montée- Plafond de propulsion
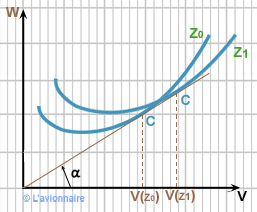
Influence de l'altitude sur le vol au maxi-range
La vitesse du maxi-range augmente avec l'altitude.
Nous avons : `Cd \text{mini} = Csp\frac{Wu}{V} = Csp\frac{Wn}{V}\text{mini} `
Influence du poids mg
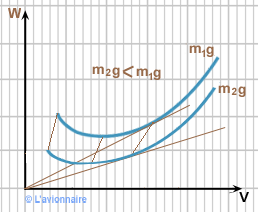
Influence de mg sur Wn = ƒ (V)
Si nous traçons deux courbes ` Wn = ƒ (V)` pour une incidence donnée et pour deux poids différents ` m_1 g` et ` m_2 g` , nous constatons un décalage vers le bas et vers la gauche pour une diminution du poids (cas du délestage en vol dû à la consommation de carburant).
Influence de mg sur la vitesse minimale
Reprenons les équations : `Wn =\sqrt\frac{2}{ρS}\times(mg)^\frac{3}{2}\times\frac{Cx}{Cz3/2}` et `V =\sqrt\frac{2mg}{ρSCz}`
Si `mg` diminue la Vitesse mini diminue également ainsi que `Wn`.
Influence de mg sur le vol à la puissance minimale
La `Wn` diminue avec la diminution de `mg` .
La consommation horaire : `C_H =\frac{Csp}{ηh}\times Wu=\frac{Csp}{ηh}\timesWn`
Si `Wn` diminue `C_H` diminue également.
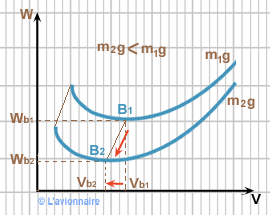
La vitesse d'autonomie maximale diminuera et l'incidence reste constante :
`\frac{Cx}{Cz3/2}\text {minimal}`
Influence de mg sur le vol au maxi-range
La consommation distance minimale diminue avec le délestage.
`Cd=\frac{Csp}{ηh}tanα` `tanα=\frac{Wn}{V} =\frac{mg}{ ƒ}`
Si `mg` diminue `Wn` diminue et la vitesse diminue également.
L'incidence reste constante et reste égale à l'incidence de finesse maximale.
Influence des volets hypersustentateurs
Le braquage des volets modifie les coefficients `Cz` et `Cx` donc de la polaire.
et du `Cx`.
Pour un braquage important des volets toujours à incidence constante, nous aurons une augmentation du `Cz` mais nous aurons une augmentation plus importante du `Cx`.
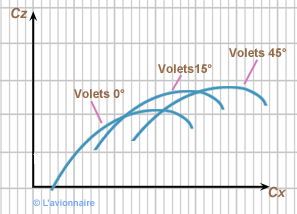
Donc pour un faible braquage, `Wn` augmente un peu et les vitesses diminuent fortement.
Et pour un fort braquage, `Wn` augmente fortement et les vitesses diminuent fortement.