
AÉRODYNAMIQUE
L'aile en supersonique
- Bang supersonique
- Cône de choc
- Théorie d'Ackeret
- Ecoulement sur un profil
- Finesse en fonction du Mach
- Influence du Mach sur le Cx
Ondes de choc
Imaginons une masse d'air dans un état de repos, et introduisons une perturbation due à l’émission instantanée d’une
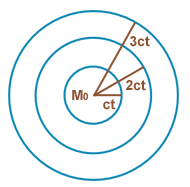
secousse unique comme un choc (détonation). Cette propagation illustrée Figure ci-dessous est observable aux instants t, 2t, 3t, après l’émission. Les observateurs situés sur des sphères de rayons ct, 2ct, 3ct, perçoivent successivement cette information dont l’amplitude sera progressivement atténuée.
Maintenant prenons un avion qui vole à une vitesse V dans une atmosphère que nous supposons infinie dans toutes les directions. Nous supposons aussi que l’atmosphère est au repos et que toutes ses propriétés physiques sont invariantes. Dans ces conditions simplifiées, la célérité des ondes sonores c est elle aussi invariante.
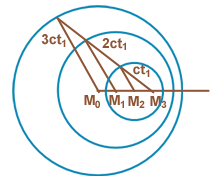
Plaçons-nous à l’instant t = 3t1, où t1 désigne un pas de temps fixé. Les fronts d’ondes qui ont quitté la source à l’instant initial, quand l’avion était en M0, ont atteint la sphère de rayon 3ct1 centrée en M0. Ceux qui ont quitté l’avion à l’instant t1 se sont propagés pendant la durée 2t1 à partir du point M1 et ont atteint la sphère de rayon 2ct1 centrée en M1, à la distance M0 M1 = Vt1 de l’origine. Ceux qui ont quitté l’avion à l’instant 2t1 se sont propagés pendant la durée t1 à partir du point M2 et ont atteint la sphère de rayon ct1 centrée en M2 , à la distance M0 M2 = 2Vt1 de l’origine.
On constate Figure ci-dessous que les sphères ne sont plus concentriques, mais excentrées et nichées les unes dans les autres.
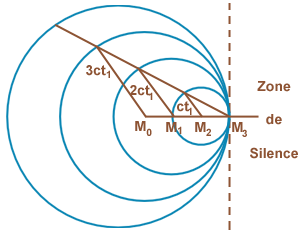
Dans le cas limite des vols exactement sonique, où V = c, les déplacements de la source M0 M1 ou M0 M2 sont égales au transit des fronts d’ondes. En conséquence, comme le montre la Figure ci-dessous, ceux-ci sont des sphères excentrées qui ne se coupent pas.
Dans le cas extrême des vols supersoniques, où V > c, le point important est la comparaison entre le transit de l’avion pendant un pas de temps t1, égal à Vt1, et le transit du front d’onde, égal à ct1. Il est clair qu’en régime supersonique le premier est plus grand que le second et qu’en conséquence, les fronts d’ondes sphériques doivent se couper. La Figure ci-dessous montre qu’ils ont alors une enveloppe commune, que l’on appelle le cône de Mach, dont le demi angle au sommet α est tel que sin α = c/V.
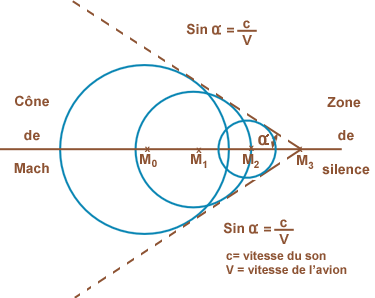
Le milieu situé à l’extérieur du cône de Mach est une zone de silence et de repos, où l’observateur ignore encore qu’un avion s’approche. Le son n’y parvient qu’avec l’onde de choc, qui constitue la frontière du cône de Mach et qui est solidaire de l’avion. Une importante énergie sonore s’est concentrée sur cette frontière, où les ondes acoustiques émises auparavant se sont rattrapées et se cumulent en formant le bang.
Le paragraphe ci-dessus est extrait d'Ondes acoustiques dans les fluides compressibles de Moreau René
Disponible sur : site pap-ebook du livre « l’air et l’eau » de Moreau René © 2013, Grenoble Sciences
Bang supersonique
Le bang supersonique n'est pas causé par le franchissement du mur du son, mais par la propagation d'une onde de choc derrière l'avion lorsque sa vitesse est supérieure à celle du son. Ce n'est pas une déflagration unique, mais une série continue de déflagrations qui dure tant que l'avion se maintient à une vitesse supersonique. Quand la frontière de la sphère provoquée par l'onde de choc atteint un point de la terre, l'observateur qui s'y trouve entend le bruit de l'avion comme si celui-ci était encore à l'endroit où le son a été émis, mais l’avion se trouve déjà à une autre position et crée une autre onde de choc. Ce retard est d’autant plus important que l’avion vole vite et haut.

Le bang est donc la “trace” au sol des ondes de compression-dépression engendrées par le déplacement supersonique de l’avion.
Cône de l'onde de choc
Celle-ci est alors délimitée par un cône (dit cône de Mach), dont le sinus du demi-angle au sommet est donné par le rapport des vitesses de l’onde et de l’avion. Plus il est rapide et plus le cône est étroit.
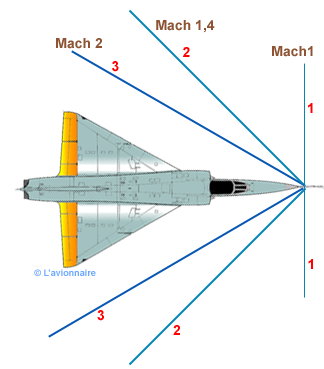
Nous avons vu ci-dessus que le sin α = c/V (vitesse du son/vitesse avion)
En 1 l'avion vole à Mach 1 c'est-à-dire à la vitesse du son. Soit 1/M = 1 donc sinus α = 1 et α = 90°
En 2 l'avion vole à Mach 1.4. Soit 1/M = 1/1.4 donc sinus α = 0,715 et α = 45°6
En 3 l'avion vole à Mach 2. Soit 1/M = 1/2 donc le sinus α = 0,5 et α = 30°
Note : Les mêmes calculs peuvent se faire en mètres/sec, en Km/H ou en Kts.
Facteurs influents sur l'onde de choc
La force de l'onde de choc émise par un avion volant à une vitesse supersonique dépend de multiples facteurs :
- Forme, taille et poids de l'avion.
- vitesse atteinte et altitude de vol.
L'onde de choc augmente considérablement en fonction de la vitesse et du poids de l'avion, mais elle diminue avec l'altitude du fait de la moindre résistance de l'air.
Généralement un avion produit plusieurs ondes de choc (au nez et à la queue) qui selon la configuration de l'appareil pourront ou non se réunir à un moment de leurs parcours.
La force originelle de l'onde de choc est progressivement atténuée par la résistance de l'air, mais il faut compter environ 40 km dans des conditions normales pour la voir se dissiper totalement.
Théorie d'Ackeret
Dans un fluide parfait (pas de frottements) pour un profil (` λ = ∞ ⇒ Cx_i = 0` ), Ackeret a démontré les résultats suivants relatifs uniquement aux forces de pressions `\vec{n}`
Portance en supersonique sur une aile
La partie aux frottements est généralement défavorable mais faible.
`Cz_\text{total}` est sensiblement égal au `Cz_n` dû aux seules forces de pressions.
Donc `Cz_\text{total} = Cz` et
`Cz = frac{4}\sqrt{\M_0^2-1}\timesα`
Traînée en supersonique sur une aile
Nous avons vu dans la partie traînée que :
`Cx_\text{total} = Cx_p + Cx_i` avec `Cx_p = Cx_f + Cx_n`
- `Cx_p` coefficient de traînée parasite
- `Cx_i` coefficient de trainée induite
- `Cx_f` coefficient de traînée de forme
- `Cx_n` coefficient aux forces de pression
L'absence de tourbillons marginaux en supersonique annule le dernier terme et
`C_\text{total}= Cx_f_ + Cx_n`
La formule D'Ackeret donne uniquement `Cx_n`
`Cx_n = frac{4}\sqrt{\M_0^2-1} (α^2 + B)` soit `Cx_n=Cz.α+ frac{4B}\sqrt{\M_0^2-1}`

D'ou l'intérêt en supersonique d'utiliser des profils à épaisseur relative faible (Concorde 3 % à l'encastrement et 1,82 % au saumon). Les profils supersoniques auront des bords d'attaque anguleux ou à très faible rayon de courbure.
Écoulement supersonique sur un profil
Écoulement sur un profil losangique
Sur un profil en losange il y a : formation d’un choc oblique attaché au bord d’attaque supérieur, en raison de la présence d’un coin concave formé par la ligne de courant qui arrive au nez du profil et le segment AB de ce profil, et d’un choc oblique symétriquement attaché au bord d’attaque inférieur, au niveau du coin concave formé par cette même ligne de courant et le segment AD du profil ; création d’une onde de détente supersonique centrée sur le sommet B du coin convexe formé par les segments AB et BC, et d’une onde symétrique centrée sur le sommet D ; enfin, création de chocs obliques au bord de fuite du profil. Dans le contexte de fluide parfait les forces aérodynamiques exercées sur un profil proviennent exclusivement des contraintes de pression.
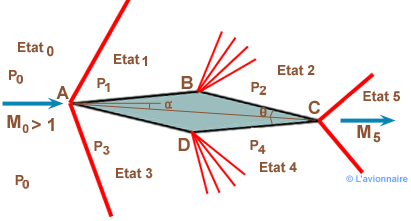
L'incidence α < θ/2 nous avons en :
Etat 1 : P 1 > P0 et M 1 < M0
Etat 3 l'onde de choc étant oblique le choc est plus important qu'en 1 donc
P3 > P1 > P0 et M3 < M 1 < M0
Etat 2 : P2 < P1 et M2 > M1
Etat 4 : P4 < P3 et M4 > M3
Les ondes de choc obliques de queue raccordent l'état 2 et l'état 4 sur l'infini aval état 5 donc
M2 > M5 et M4 > M5 puisque M5 = M0 > 1
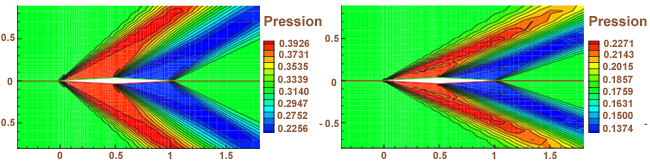
Isovaleurs sur un profil losangique de rapport épaisseur / corde 0.07 pour une incidence égale et un nombre de Mach 1.5 (gauche) et Mach 2 (droite)
Écoulement sur un profil à bord d'attaque arrondi
L'onde de choc de tête est détachée du bord d'attaque. Une zone inférieure à Mach 1 se forme devant le bord d'attaque au point de stagnation.
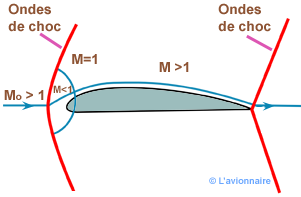
Ci-dessous : configuration montrant la présence d'un choc détaché à l'amont d'un obstacle de demi-angle de 10° dans un écoulement à nombre de Mach 1.3

Finesse en fonction du Mach
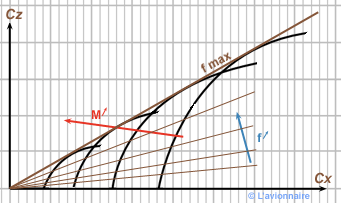
`\frac{Cz}{Cz}=ƒ`. La finesse est donc indépendante du nombre de Mach. Les iso-incidences sont des droites.
Influence du nombre de Mach sur le Cx
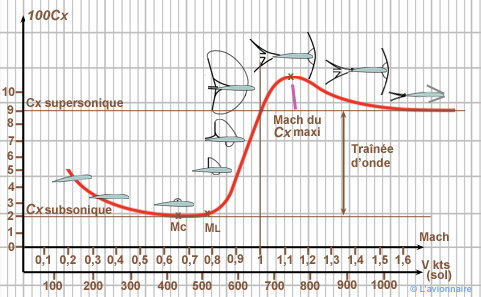
En prenant la courbe de Cx en fonction du Mach sur Concorde (ci-dessous), on constate que lorsque la vitesse augmente, comme mg est égal à Rz l'incidence change. La courbe des Cx débutant à la vitesse mini de sustentation va commencer par décroître, puis stabilisé jusqu'au Mach critique. Passé la Mach limite ou Mach de divergence le Cx augmente considérablement pour atteindre le Mach du Cx maxi vers Mach 1.1. Puis le Cx diminue pour se stabiliser ensuite aux alentours de Mach 1.4
Résumé
Sans entrer plus avant dans les détails, on notera seulement :
- En subsonique, la polaire est habituellement indépendante du Mach. En transsonique et en
supersonique, elle dépend du nombre de Mach.
- L’accroissement de la traînée au passage de Mach 1.
- La diminution du coefficient de portance maximale et du moment de tangage liée à la forme
du profil à partir du régime transsonique.
- Le recul du foyer en supersonique.
